Координаты вектора. Векторы называются линейно зависимыми, если они удовлетворяют равенству

Векторы 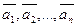называются линейно зависимыми, если они удовлетворяют равенству

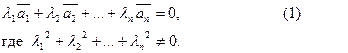
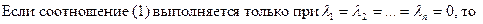
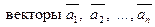называются линейно независимыми.

Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны, т.е. параллельны одной прямой.

Три вектора линейно зависимы тогда и только тогда, когда они компланарны, т.е. параллельны одной плоскости.

Базисом на плоскости называется любая упорядоченная пара линейно независимых векторов 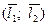. Любой вектор 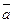на плоскости можно единственным образом разложить по базису, т.е. представить в виде

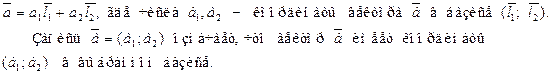Базисом в пространстве называется любая упорядоченная тройка линейно независимых векторов 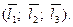Любой вектор 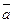в пространстве можно единственным образом представить в виде

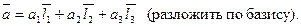
Числа а ₁, а ₂, а ₃ называются координатами вектора 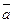в выбранном базисе. Записывается это так: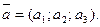

Ортонормированным базисом называется базис из взаимно перпендикулярных векторов единичной длины. Ортонормированный базис на плоскости будем обозначать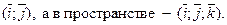

Если в некотором базисе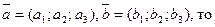

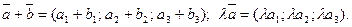
Два ненулевых вектора 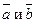коллинеарны тогда и только тогда, когда 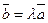или b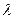_i = a_{i ,}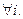

Три вектора 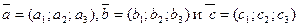компланарны тогда и только тогда, когда