Прямая и плоскость.
Любая прямая на плоскости определяется линейным уравнением
Ах + Ву + С = 0, А2 + В2 ≠ 0, (9)
которое называется общим уравнением прямой (здесь А и В – координаты вектора нормали 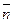 , перпендикулярного этой прямой).
, перпендикулярного этой прямой).
Если прямая задается точкой М (х 1; у 1) и вектором нормали 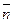 = (А; В), то ее уравнение запишется в виде
= (А; В), то ее уравнение запишется в виде
А (х – х 1) + В (у – у 1) = 0. (10)
Уравнение прямой, проходящей через две точки М (х 1; у 1) и N (х 2; у 2) имеет вид:

Частным случаем этой формулы является уравнение прямой, проходящей через точки М (а; 0) и N (0; b), называемое уравнением прямой в отрезках:

Каноническим уравнением прямой

лучше пользоваться тогда, когда прямая задана точкой М (х 1; у 1) и направляющим вектором 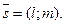
Уравнение прямой с угловым коэффициентом k имеет вид:
y = kx + b, (14)
здесь k = tgθ тангенс угла наклона прямой к оси Ох.
Уравненение прямой с угловым коэффициентом k, проходящей через точку М (х 1; у 1) имеет вид:
y – y 1 = k (x – x 1) (15)
Угол 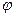 между двумя прямыми l 1 и l 2 вычисляются по формуле:
между двумя прямыми l 1 и l 2 вычисляются по формуле:

где k 1 и k 2 – угловые коэффициенты прямых l1 и l2 .
Расстояние d от точки М (х 0; у 0) до прямой, заданной уравнением Ах + Ву + С = 0, вычисляется по формуле:

Уравнение
А 1 х + В 1 у + С 1 + 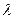 (А 2 х + В 2 у + С 2 ) = 0, (18)
(А 2 х + В 2 у + С 2 ) = 0, (18)
где 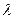 – числовой множитель, определяет прямую линию, проходящую через точку пересечения прямых
– числовой множитель, определяет прямую линию, проходящую через точку пересечения прямых
li: Аi х + Вi у + Сi = 0, i = 1; 2. (19)
При различных 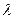 получаются различные прямые, принадлежащие пучку прямых, с центром в точке пересечения прямых l 1 и l 2.
получаются различные прямые, принадлежащие пучку прямых, с центром в точке пересечения прямых l 1 и l 2.
Пусть прямые l 1 и l 2 заданы уравнениями (19).
Условия пересечения, параллельности или совпадения этих прямых приведены в следующей таблице.
| Взаимное расположение | Условия |
| Пересекаются | 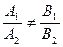
|
| Параллельны (l 1 ≠ l 2 ) | 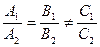
|
| Совпадают | 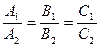
|
 2014-01-25
2014-01-25 729
729








