Смешанное произведение трех векторов

Смешанным произведением векторов 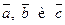называется скалярное произведение вектора 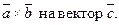Оно обозначается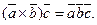

Смешанное произведение обладает следующими свойствами:

1. смешанное произведение трёх векторов равно нулю, если:

а) хотя бы один из перемножаемых векторов равен нулю;

б) два из перемножаемых векторов коллинеарны;

в) три вектора параллельны одной плоскости (компланарны);

2.

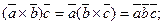
3. ;

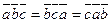4. .

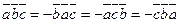Геометрический смысл смешанного произведения трёх векторов заключается в том, что его модуль равен объему параллелепипеда, построенного на этих векторах.

В базисе (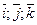) смешанное произведение векторов 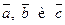имеет вид:

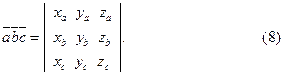
Если смешанное произведение векторов положительно, то тройка этих векторов – правая, а если отрицательно, то – левая.