Нахождение решения линейного неоднородного уравнения
Этот метод рассмотрим на примере уравнения II порядка:
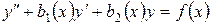 . . | (1) |
Запишем однородное уравнение, соответствующее уравнению (1):
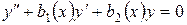 . . | (5) |
Пусть 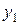 и
и 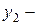 фундаментальная система решений уравнения (2), тогда его общее решение
фундаментальная система решений уравнения (2), тогда его общее решение 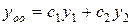 .
.
Решение уравнения (1) будем искать так: в  варьируем произвольные постоянные, т.е. будем считать их функциями от х, т.е.
варьируем произвольные постоянные, т.е. будем считать их функциями от х, т.е. 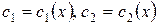 .
.
И потребуем, чтобы функция 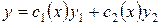 удовлетворяла уравнению (1).
удовлетворяла уравнению (1).
Вычислим производную:
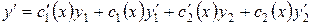 .
.
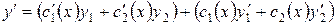 .
.
Потребуем, чтобы выполнилось равенство:
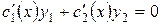 . . | (А) |
Тогда 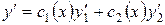 , следовательно,
, следовательно,
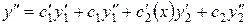 .
.
Подставляя 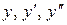 в уравнение (1), получим тождество:
в уравнение (1), получим тождество:
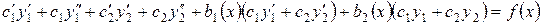 .
.
Сгруппируем слагаемые с 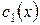 и
и 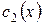 :
:
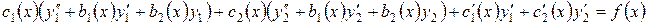
Обе скобки равны нулю, так как 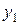 и
и 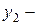 решения уравнения (2).
решения уравнения (2).
Значит, остается:
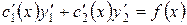 . . | (В) |
Таким образом, чтобы функция 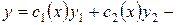 была решением уравнения (1) достаточно, чтобы выполнялись равенства (А) и (В), т.е. приходим к системе:
была решением уравнения (1) достаточно, чтобы выполнялись равенства (А) и (В), т.е. приходим к системе:
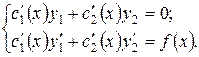 | (С) |
Функции 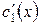 и
и 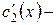 неизвестные в этой системе. Определитель этой системы – есть вронскиан решений
неизвестные в этой системе. Определитель этой системы – есть вронскиан решений 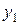 и
и 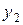 в силу фундаментальности решений
в силу фундаментальности решений 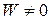 , значит, система имеет единственное решение:
, значит, система имеет единственное решение:
 .
.
Интегрируя, находим:
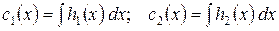 .
.
Подставляя найденные функции в общий вид решения, получаем общее решение линейного неоднородного уравнения:
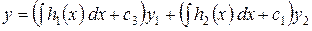 .
.
Пример. Решить уравнение: 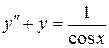 .
.
Решение. Как известно, 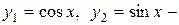 фундаментальная система решений однородного уравнения
фундаментальная система решений однородного уравнения 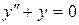 , следовательно:
, следовательно:
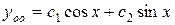 ;
;
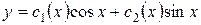 .
.
Составим систему (С):
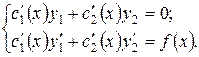
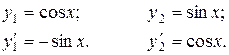
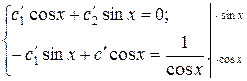
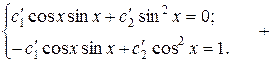
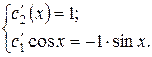
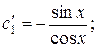
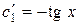 .
.
Находим 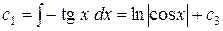 ;
; 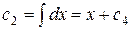 .
.
Ответ: 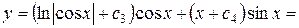
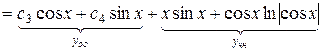 .
.
Замечание. Для линейного неоднородного уравнения более высокого порядка метод вариации произвольной постоянной применяется аналогично (система будет больше).
16. Линейные дифференциальные уравнения с постоянными
коэффициентами
16.1 Линейные однородные уравнения с постоянными коэффициентами
Определение. Линейным однородным уравнением п -го порядка с постоянными коэффициентами называется уравнение:
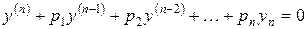 , , | (1) |
где 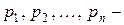 действительные числа.
действительные числа.
Будем искать решение (1) в виде 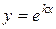 .
.
Найдем производные: 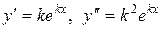
Подставляя у и его производные в уравнение (1), получим тождество:
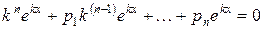 .
.
Сократив все уравнение на 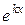 , приходим к уравнению:
, приходим к уравнению:
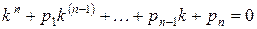 . . | (2) |
Определение. Уравнение (2) называется характеристическим уравнением уравнения (1). Характеристическое уравнение – это алгебраическое уравнение, имеющее п корней. Корни 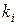 могут быть действительными или комплексными или часть действительными и часть комплексными.
могут быть действительными или комплексными или часть действительными и часть комплексными.
Таким образом, если функция 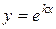 - решение уравнения (1), то число k – решение (корень) уравнения (2) и наоборот.
- решение уравнения (1), то число k – решение (корень) уравнения (2) и наоборот.
Пусть дано линейное однородное уравнение с постоянными коэффициентами:
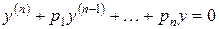 .
.
При замене:
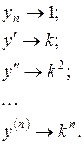
Приходим к характеристическому уравнению:
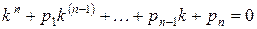 . . | (2) |
В зависимости от корней характеристического уравнения (2) будет меняться вид общего решения уравнения (1). Вопрос о структуре общего решения уравнения (1) рассмотрим на примере линейного однородного уравнения II порядка с постоянными коэффициентами:
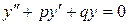 , , | (3) |
где 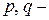 действительные числа.
действительные числа.
Его характеристическое уравнение имеет вид:
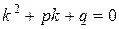 . . | (4) |
Могут представиться 3 случая.
Случай 1. Пусть корни характеристического уравнения (4) действительные и различные, т.е. 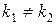 .
.
Теорема 1. Если корни характеристического уравнения действительные и различные, то общее решение уравнения (3) имеет вид:
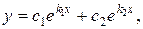
где 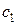 и
и 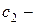 постоянные.
постоянные.
Доказательство. Пусть 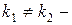 корни уравнения (4),
корни уравнения (4), 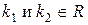 . Так как уравнение (3) частный случай уравнения (1), то согласно сказанному выше:
. Так как уравнение (3) частный случай уравнения (1), то согласно сказанному выше: 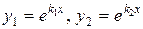 являются частными решениями уравнения (3).
являются частными решениями уравнения (3).
Найдем 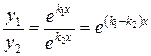 , так как
, так как 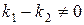 , то
, то 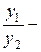 есть функция, значит
есть функция, значит 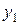 и
и 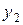 линейно независимые функции и образуют фундаментальную систему решений уравнения (3).
линейно независимые функции и образуют фундаментальную систему решений уравнения (3).
По теореме о структуре общего решения линейного уравнения (п.13) утверждаем, что общее решение (3) имеет вид:
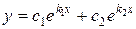 .
.
Теорема доказана.
Пример 1. 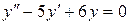 .
.
Решение. 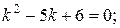
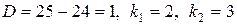 .
.
Ответ: 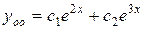 .
.
Случай 2. Пусть корни характеристического уравнения действительные и равные 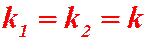 .
.
Теорема 2. Если корни характеристического уравнения (4) действительные и равные k, то общее решение уравнения (3) имеет вид:
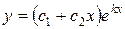 .
.
Доказательство. Пусть корни характеристического уравнения равны между собой и равны k, тогда мы знаем, что функция 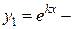 одно из решений уравнения (3) (частное). Так как уравнение второго порядка, то должно быть еще одно решение. Другое частное решение будем искать в виде:
одно из решений уравнения (3) (частное). Так как уравнение второго порядка, то должно быть еще одно решение. Другое частное решение будем искать в виде:
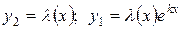 , , | (*) |
где 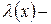 неизвестная функция,
неизвестная функция, 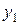 и
и 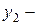 должны быть линейно независимыми.
должны быть линейно независимыми.
Найдем производные 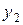 :
:
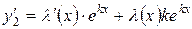 | (**) |
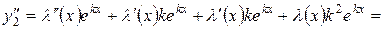 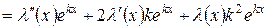 | (***) |
Подставляя равенства (*), (**), (***) в уравнение (3), получим тождество:
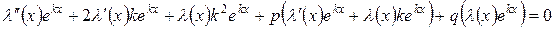 .
.
Сгруппируем слагаемые с 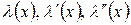 и сократим на
и сократим на 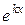 :
:
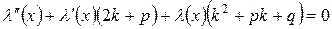 .
.
Так как 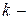 есть корень характеристического уравнения (4), то последняя скобка равна нулю, кроме того, по теореме Виета:
есть корень характеристического уравнения (4), то последняя скобка равна нулю, кроме того, по теореме Виета: 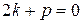 .
.
Остается 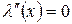 .
.
Интегрируя это уравнение 2 раза, получаем:
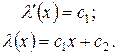
Так как мы ищем второе частное решение уравнения (3), то достаточно в последнем равенстве положить 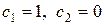 .
.
Тогда 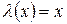 и
и 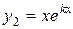 .
.
Нетрудно проверить, что 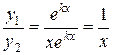 является функцией, следовательно,
является функцией, следовательно, 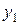 и
и 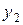 образуют фундаментальную систему решений. Тогда по теореме о структуре общего решения линейного однородного уравнения утверждаем, что:
образуют фундаментальную систему решений. Тогда по теореме о структуре общего решения линейного однородного уравнения утверждаем, что:
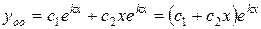 .
.
Теорема доказана.
Пример 2. 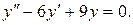
Решение. 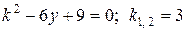 .
. 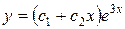 .
.
Ответ: 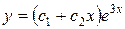 .
.
Случай 3. Пусть корни характеристического уравнения (4) комплексные: 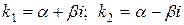 .
.
Сначала докажем лемму.
Лемма. Если функция 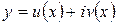 является решением уравнения (3), то ее действительная и мнимая части
является решением уравнения (3), то ее действительная и мнимая части 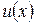 и
и 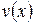 также является решениями этого уравнения.
также является решениями этого уравнения.
Доказательство. Пусть 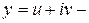 решение уравнения (3). Найдем производные и подставим их в (3):
решение уравнения (3). Найдем производные и подставим их в (3):
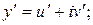
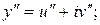
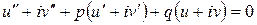 .
.
Сгруппируем все с функцией u и v:
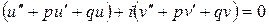 .
.
Комплексное выражение обращается в 0 тогда и только тогда, когда его действительные и мнимые части равны нулю, т.е.
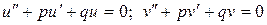 .
.
Это говорит о том, что 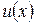 и
и 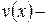 решения уравнения (3).
решения уравнения (3).
Лемма доказана.
Теорема 3. Если корни характеристического уравнения комплексные 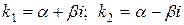 , то общее решение уравнения (3) имеет вид:
, то общее решение уравнения (3) имеет вид:
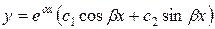 .
.
Доказательство. Пусть 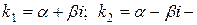 корни характеристического уравнения (4). Им соответствуют частные решения уравнения (3):
корни характеристического уравнения (4). Им соответствуют частные решения уравнения (3):
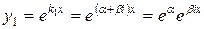 ;
;
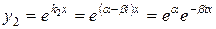 .
.
По формулам Эйлера имеем:
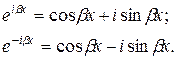
Тогда:
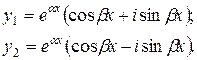
Раскрывая скобки, получим:
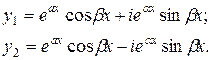
Эти функции являются решением (3), но тогда по лемме их действительные и мнимые части также являются решениями уравнения (3).
Таким образом, мы можем взять два частных решения уравнения (3):
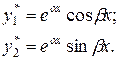
Эти решения линейно независимы, т.к. 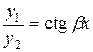 . Значит, они образуют фундаментальную систему решений уравнения (3). По теореме о структуре общего решения линейного однородного уравнения II порядка имеем:
. Значит, они образуют фундаментальную систему решений уравнения (3). По теореме о структуре общего решения линейного однородного уравнения II порядка имеем:
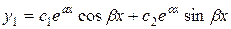 , или
, или
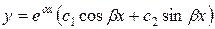 .
.
Теорема доказана.
Замечание. Если корни характеристического уравнения чисто мнимые 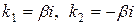 , то полагаем
, то полагаем 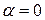 и решение имеет вид:
и решение имеет вид:
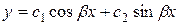 .
.
Пример 3. 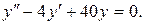
Решение. 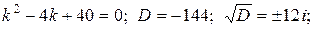
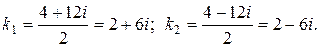
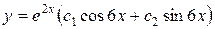 .
.
Ответ: 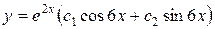 .
.
Обобщим все сказанное выше об уравнении II порядка на линейное однородное уравнение п -го порядка с постоянными коэффициентами. Запишем уравнение:
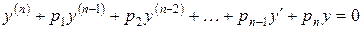 . . | (1) |
Его общее решение находится так: записываем характеристическое уравнение, соответствующее уравнению (1), и находим его корни.
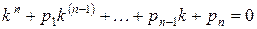 . . | (2) |
где 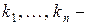 корни.
корни.
Частные решения уравнения (1) находим, руководствуясь правилами:
а) если 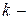 простой действительный корень уравнения (2), то ему соответствует одно частное решение уравнения (1) вида:
простой действительный корень уравнения (2), то ему соответствует одно частное решение уравнения (1) вида:
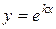 .
.
б) если 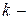 действительный корень характеристического уравнения (2) кратности s, то этому корню соответствуют s линейных независимых частных решений уравнения (1) вида:
действительный корень характеристического уравнения (2) кратности s, то этому корню соответствуют s линейных независимых частных решений уравнения (1) вида:
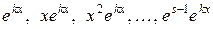 .
.
в) если 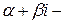 простой комплексный корень уравнения (2), то сопряженное число
простой комплексный корень уравнения (2), то сопряженное число 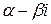 также простой комплексный корень уравнения (2). Этой паре комплексных чисел соответствуют два линейных независимых частных решения:
также простой комплексный корень уравнения (2). Этой паре комплексных чисел соответствуют два линейных независимых частных решения:
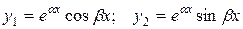 .
.
г) если 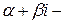 корень уравнения (2) кратности т, то
корень уравнения (2) кратности т, то 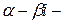 корень уравнения (2) кратности т. Этой паре комплексно сопряженных корней соответствует 2 т линейно независимых частных решений уравнения (1):
корень уравнения (2) кратности т. Этой паре комплексно сопряженных корней соответствует 2 т линейно независимых частных решений уравнения (1):
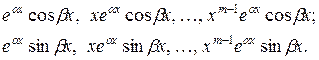
Следуя пунктам а) – г), мы найдем п линейно независимых решений уравнения (1), а, сложив их, получим общее решение:
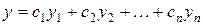 .
.
Пример 4. 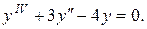
Решение. 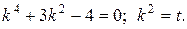
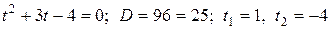 .
.


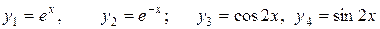 .
.
Ответ: 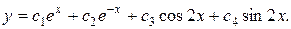
 2014-01-25
2014-01-25 1262
1262
