Теорема 1 (без доказательства). Если 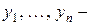 система функций, являющихся линейно зависимыми на промежутке
система функций, являющихся линейно зависимыми на промежутке 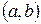 , то определитель Вронского этой системы равен 0 для любого
, то определитель Вронского этой системы равен 0 для любого 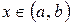 .
.
Теорема 2 (без доказательства). Если 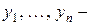 система п линейно независимых частных решений линейного однородного уравнения
система п линейно независимых частных решений линейного однородного уравнения
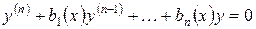 , , | (1) |
то определитель Вронского этой системы не обращается в нуль ни в одной точке интервала 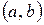 .
.
Теорема 3 (без доказательства). Если 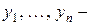 система частных решений однородного уравнения (1), то определитель Вронского этой системы либо равен нулю для любого
система частных решений однородного уравнения (1), то определитель Вронского этой системы либо равен нулю для любого 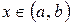 , либо не равен нулю ни в одной точке из интервала
, либо не равен нулю ни в одной точке из интервала 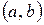 .
.
12. Фундаментальная система решений
Определение. Любая совокупность п линейно независимых частных решений линейного однородного уравнения
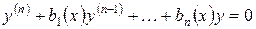 , , | (1) |
называется фундаментальной системой решений этого уравнения.
Замечание. Пусть имеем систему из двух функций 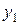 и
и 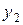 . Эта система будет линейно зависимой, если отношение
. Эта система будет линейно зависимой, если отношение 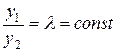 , и линейно независимой, если
, и линейно независимой, если 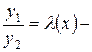 функция.
функция.
13. Теорема о структуре общего решения линейного однородного уравнения
Теорема. Если 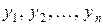 есть фундаментальная система решений линейного однородного уравнения
есть фундаментальная система решений линейного однородного уравнения
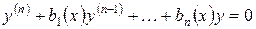 , , | (1) |
то его общее решение имеет вид:
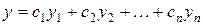 ,
,
где 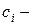 произвольные постоянные.
произвольные постоянные.
Доказательство. Проведем его для линейного однородного уравнения третьего порядка:
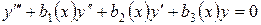 . . | (*) |
Пусть 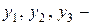 фундаментальная система решений этого уравнения. Требуется доказать, что функция
фундаментальная система решений этого уравнения. Требуется доказать, что функция 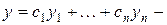 общее решение уравнения (*). По теореме 3 (п.9 свойства решения однородного уравнения) эта функция является решением уравнения (*) при любом
общее решение уравнения (*). По теореме 3 (п.9 свойства решения однородного уравнения) эта функция является решением уравнения (*) при любом 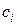 . Чтобы показать, что эта функция является общим решением, остается доказать, что если заданы начальные условия
. Чтобы показать, что эта функция является общим решением, остается доказать, что если заданы начальные условия 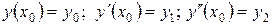 , то
, то 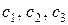 можно подобрать так, чтобы эти начальные условия выполнялись.
можно подобрать так, чтобы эти начальные условия выполнялись.
Найдем производные решения и подставим начальные данные. Получим систему:
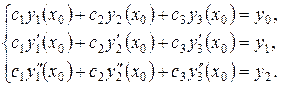
Эта система линейная с тремя неизвестными 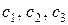 . Определитель этой системы – это определитель Вронского для системы функций
. Определитель этой системы – это определитель Вронского для системы функций 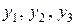 вычисленный в точке
вычисленный в точке 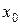 .
.
Так как система 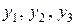 - фундаментальная, то
- фундаментальная, то 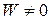 , следовательно, система имеет единственное решение:
, следовательно, система имеет единственное решение:
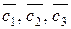
Функция 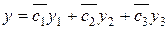 будет удовлетворять начальным условиям.
будет удовлетворять начальным условиям.
По определению общего решения (понятие общего решения п. 6) мы утверждаем, что эта функция действительно общее решение уравнения (*). Теорема доказана.
Пример. Найти общее решение уравнения 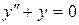 , если частные решения
, если частные решения 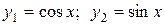 .
.
Решение. Отношение 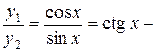 функция, следовательно,
функция, следовательно, 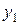 и
и 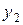 линейно независимы и образуют фундаментальную систему решений.
линейно независимы и образуют фундаментальную систему решений.
Значит, общее решение имеет вид:
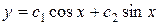 .
.
 2014-01-25
2014-01-25 1066
1066
