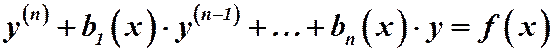 (1)
(1)
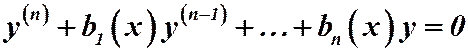 (2)
(2)
обозначим через 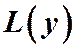 , т.е.
, т.е. 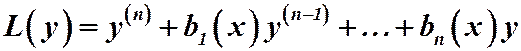 .
.
Тогда уравнения (1) и (2) перепишутся в виде:
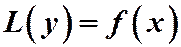
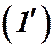
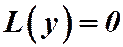
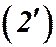
Определение. Выражение 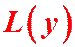 называется линейным дифференциальным оператором.
называется линейным дифференциальным оператором.
Теорема 1. Если 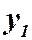 и
и 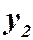 суть частные решения линейного однородного уравнения (2), то их сумма
суть частные решения линейного однородного уравнения (2), то их сумма 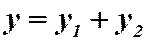 есть также решение этого уравнения.
есть также решение этого уравнения.
Доказательство. Проведем доказательство для уравнения третьего порядка 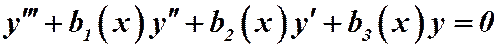 (3)
(3)
Пусть 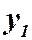 и
и 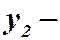 решения этого уравнения, тогда
решения этого уравнения, тогда 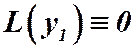 ,
, 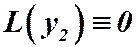 .
.
Требуется доказать, что функция 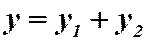 есть также решение уравнения (3). Ясно, что если
есть также решение уравнения (3). Ясно, что если 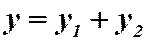 , то
, то 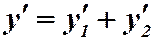 ;
; 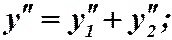
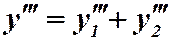 . Поэтому:
. Поэтому: 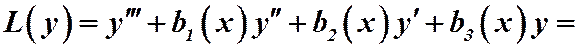
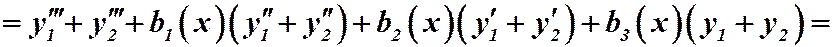
Перегруппируем слагаемые:
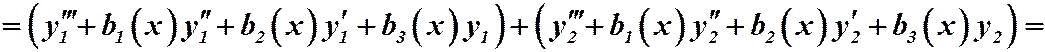
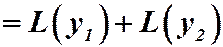 .
.
Получим, что  . И так как
. И так как 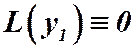 и
и 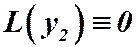 , то
, то 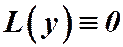 . Значит, функция
. Значит, функция 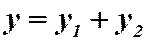 есть решение уравнения (3).
есть решение уравнения (3).
Теорема доказана.
Аналогично, если 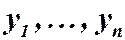 являются решениями линейного однородного уравнения (2), то функция
являются решениями линейного однородного уравнения (2), то функция 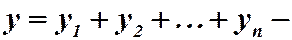 есть также решение этого уравнения.
есть также решение этого уравнения.
Теорема 2. Если 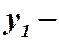 есть решение линейного однородного уравнения (2), С – произвольная постоянная, то функция
есть решение линейного однородного уравнения (2), С – произвольная постоянная, то функция 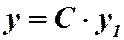 есть также решение уравнения (2).
есть также решение уравнения (2).
Доказательство. Если 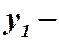 решение (2), то
решение (2), то 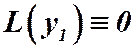 .
.
Если 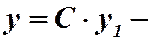 предполагаемое решение (2), то
предполагаемое решение (2), то 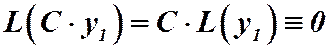 , следовательно,
, следовательно, 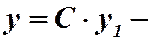 действительно решение. Теорема доказана.
действительно решение. Теорема доказана.
Теорема 3. Если 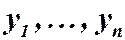 суть частные решения линейного однородного уравнения (2), а
суть частные решения линейного однородного уравнения (2), а 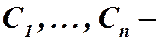 произвольные постоянные, то функция
произвольные постоянные, то функция 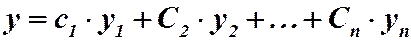 также решение уравнения (2) (следствие теорем 1 и 2).
также решение уравнения (2) (следствие теорем 1 и 2).
10. Линейные зависимые и линейные независимые системы функций
Пусть дана система функций
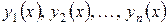 , ,
| (1) |
определенных в некотором интервале 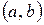 .
.
Определение. Система функций (1) называется линейно зависимой в интервале 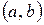 , если существуют числа
, если существуют числа 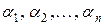 не все равные нулю, такие что для всех х из
не все равные нулю, такие что для всех х из 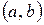 выполняется равенство:
выполняется равенство:
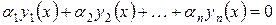 . .
| (2) |
Если равенство (2) для любого 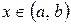 выполняется в том случае, когда все коэффициенты
выполняется в том случае, когда все коэффициенты 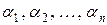 равны нулю, то система функций (1) называется линейно независимой в промежутке
равны нулю, то система функций (1) называется линейно независимой в промежутке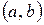 .
.
Пример. 1) Рассмотрим систему функций: 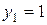 ;
; 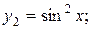
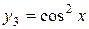 .
.
Функции 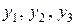 определены в
определены в 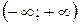 . Запишем (2):
. Запишем (2):
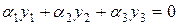 .
.
Положим в качестве чисел 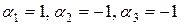 , получим:
, получим:
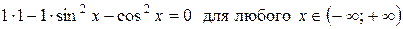 .
.
Значит, система функций является линейно зависимой.
2) Запишем систему из 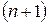 функций:
функций:
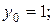
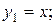
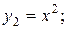
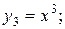
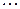
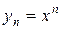
Запишем равенство (2):
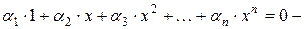
это есть алгебраическое уравнение (п)-ой степени, которое имеет п корней. Значит, это равенство может выполняться не более чем при п значениях х, а не при любом х. Следовательно, все коэффициенты 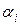 должны быть равны нулю. Данная система является линейно зависимой системой функций.
должны быть равны нулю. Данная система является линейно зависимой системой функций.
11. Определитель Вронского и его свойства
Пусть дана система функций 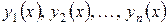 , определенных в интервале
, определенных в интервале 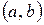 и имеющих в нем все производные до
и имеющих в нем все производные до 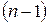 порядка включительно.
порядка включительно.
Запишем определитель:
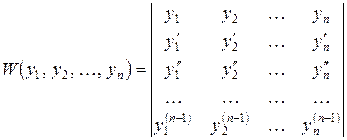 .
.
Определение. Этот определитель называется определителем Вронского данной системы функций (вронскиан).
Очевидно, что вронскиан – это функция от х, т.е. 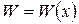 .
.
Пример. Дано 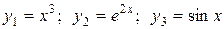 . Составить определитель Вронского.
. Составить определитель Вронского.
Решение.
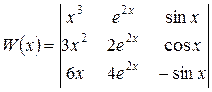 .
.
Прежде чем говорить о свойствах вронскиана, докажем теорему.
Теорема. Если система функций 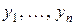 является линейно зависимой на промежутке
является линейно зависимой на промежутке 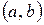 , то одну из функций этой системы всегда можно представить линейной комбинацией остальных функций, т.е.
, то одну из функций этой системы всегда можно представить линейной комбинацией остальных функций, т.е.
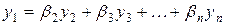 .
.
Доказательство. Пусть система функций является линейно зависимой, тогда для любого 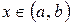 выполняется равенство:
выполняется равенство:
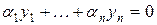 ,
,
где не все 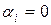 .
.
Пусть 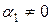 , тогда поделив все равенство на
, тогда поделив все равенство на 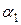 , найдем
, найдем 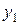 :
:
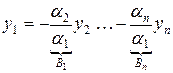 .
.
Мы видим, что 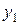 линейно выражается через все остальные.
линейно выражается через все остальные.
Теорема доказана.
 2014-01-25
2014-01-25 782
782








