Построение множества комплексных чисел.
Число – одно из фундаментальных понятий математики. Из школьного курса математики нам известны натуральные, целые, рациональные и действительные числа. Давайте вспомним, каким образом в истории математики происходило развитие понятия числа и что способствовало появлению новых числовых множеств на каждом этапе ( ).
).
В 16 в встает проблема, которая связана с неразрешимостью на множестве действительных чисел уравнений типа 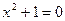 . Таким образом, появляется необходимость в расширении множества
. Таким образом, появляется необходимость в расширении множества 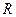 так, чтобы в новой числовой системе было разрешимо уравнение указанного типа и сохранялись все свойства операций над действительными числами. Впервые решение этой проблемы предложили итальянские математики Кардано и Бомбелли. Далее мы восстановим их рассуждения.
так, чтобы в новой числовой системе было разрешимо уравнение указанного типа и сохранялись все свойства операций над действительными числами. Впервые решение этой проблемы предложили итальянские математики Кардано и Бомбелли. Далее мы восстановим их рассуждения.
Рассмотрим множество упорядоченных пар действительных чисел
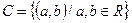 ,
,
и назовем элементы этого множества комплексными числами. На множестве комплексных чисел зададим операции сложения и умножения:
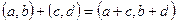 и
и 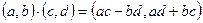 .
.
Покажем, что построенная числовая система удовлетворяет указанным выше условиям. Во-первых, любое действительное число a можно рассматривать как пару 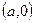 , а значит, множество
, а значит, множество 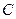 содержит действительные числа. Во-вторых,
содержит действительные числа. Во-вторых, 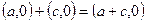 ,
, 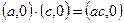 .
.
Теорема (свойства операций на множестве комплексных чисел)
1. Сложение комплексных чисел коммутативно, ассоциативно.
2. Умножение комплексных чисел коммутативно, ассоциативно, дистрибутивно относительно сложения.
3. Нулем на множестве комплексных чисел является пара 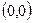 .
.
4. Для каждого комплексного числа есть противоположное число.
5. Единицей на множестве комплексных чисел является пара 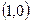 .
.
6. Для каждого ненулевого комплексного числа есть обратное число.
7. На множестве комплексных чисел разрешимо уравнение 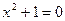 .
.
Доказательство. 1) Покажем, что сложение на множестве C коммутативно: 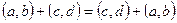 . Действительно,
. Действительно,
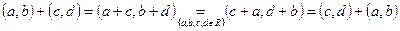 .
.
Покажем, что сложение на множестве C ассоциативно: 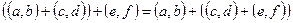 . Действительно,
. Действительно,
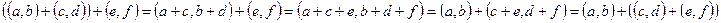 2) Коммутативность и ассоциативность умножения докажите самостоятельно. Покажем, что умножение дистрибутивно относительно сложения на множестве комплексных чисел:
2) Коммутативность и ассоциативность умножения докажите самостоятельно. Покажем, что умножение дистрибутивно относительно сложения на множестве комплексных чисел: 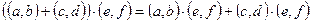 . Преобразуем левую часть тождества:
. Преобразуем левую часть тождества: 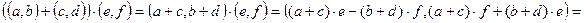
 . Преобразуем правую часть тождества:
. Преобразуем правую часть тождества:
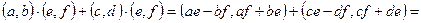
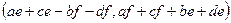 . Легко видеть, что левая и правая части равны.
. Легко видеть, что левая и правая части равны.
3) Покажем, что 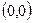 – ноль на множестве комплексных чисел:
– ноль на множестве комплексных чисел:
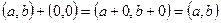 .
.
4) Покажем, что противоположным для комплексного числа 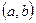 является число
является число 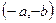 . Действительно,
. Действительно, 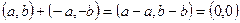 .
.
5) Самостоятельно докажите, что 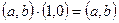 .
.
6) Покажем, что любое комплексное число 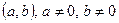 имеет обратное. Если
имеет обратное. Если 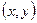 – число, обратное для
– число, обратное для 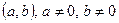 , то
, то 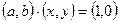 . Преобразуя последнее равенство, получим систему уравнений с двумя неизвестными:
. Преобразуя последнее равенство, получим систему уравнений с двумя неизвестными:  Откуда находим
Откуда находим  ,
, 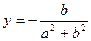 . Таким образом,
. Таким образом, 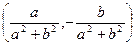 – число, обратное для
– число, обратное для 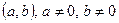 .
.
7) Рассмотрим уравнение 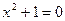 . На множестве C оно примет вид
. На множестве C оно примет вид  ,
, 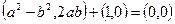 ,
, 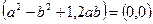 . Получили систему уравнений с двумя неизвестными
. Получили систему уравнений с двумя неизвестными 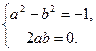 , решениями которой являются пары
, решениями которой являются пары 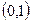 и
и  ■
■
Комплексное число 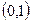 называют мнимой единицей.
называют мнимой единицей.
 2014-01-25
2014-01-25 1155
1155








