Действия над комплексными числами в алгебраической форме записи.
Алгебраическая форма записи комплексного числа.
Форма записи комплексных чисел, предложенная Кардано и Бомбелли, неудобна для выполнения над ними арифметических операций. В 18 веке Эйлер предложил ввести обозначение: 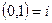 , т.е., i – корень уравнения
, т.е., i – корень уравнения 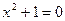 на множестве C. Теперь комплексное число
на множестве C. Теперь комплексное число 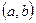 можно записать в виде
можно записать в виде 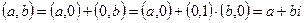 .
.
Запись комплексного числа в виде 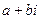 называется алгебраической. Число
называется алгебраической. Число 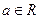 называется его действительной частью и обозначается
называется его действительной частью и обозначается 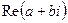 , число
, число 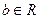 – мнимой частью и обозначается
– мнимой частью и обозначается 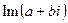 .
.
Очевидно, что два комплексных числа равны тогда и только тогда, когда равны их действительные и мнимые части соответственно.
В силу свойств операций над комплексными числами, действия над комплексными числами в алгебраической форме записи можем выполнять так же, как с алгебраическими выражениями. Приведем примеры (найти сумму, разность, произведение и частное комплексных чисел).
Определение. Сопряженным для комплексного числа называется число, действительная часть которого равна действительной части данного числа, а мнимая часть противоположна по знаку.
Обозначение: 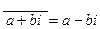 .
.
Теорема (свойства сопряженных комплексных чисел). Пусть 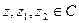 .
.
1. 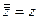 , 2.
, 2. 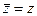 ,если
,если 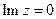 , 3.
, 3. 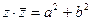 ,
,
4. 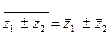 , 5.
, 5. 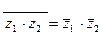 , 6.
, 6. 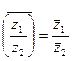 ,
, 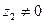 .
.
Доказательство. 1) Пусть 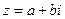 . Тогда
. Тогда 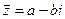 и
и 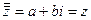 .
.
2) Если 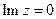 , то
, то 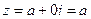 , а значит,
, а значит, 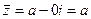 .
.
3) Пусть 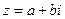 . Тогда
. Тогда 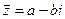 и
и 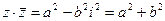 .
.
4) Пусть 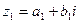 ,
, 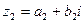 . Тогда
. Тогда 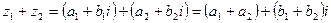 и
и 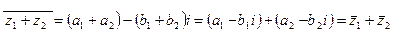 .
.
5) Докажите самостоятельно.
6) Докажите самостоятельно ■
Геометрическая иллюстрация комплексных чисел.
 2014-01-25
2014-01-25 1034
1034
