Определение. Тригонометрической формой записи комплексного числа 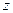 называется представление его в виде
называется представление его в виде
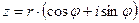 ,
,
где 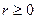 , а
, а 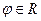 . Число r называется модулем комплексного числа z и обозначается
. Число r называется модулем комплексного числа z и обозначается 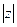 , а
, а 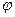 называется аргументом комплексного числа z и обозначается
называется аргументом комплексного числа z и обозначается 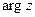 .
.
Возникают вопросы. Во-первых, любое ли комплексное число можно представить в тригонометрической форме. Во-вторых, как перейти от алгебраической формы записи к тригонометрической. Ответы на эти вопросы дает следующая теорема.
Теорема (о представлении комплексного числа в тригонометрической форме записи).
Всякое комплексное число 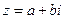 можно представить в тригонометрической форме записи. Если
можно представить в тригонометрической форме записи. Если 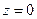 , то
, то 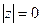 , а аргумент
, а аргумент 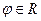 . Если
. Если 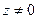 , то его модуль находится однозначно, а аргумент – с точностью до слагаемого, кратного
, то его модуль находится однозначно, а аргумент – с точностью до слагаемого, кратного 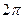 :
:
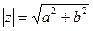 , а
, а 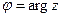 задается условиями
задается условиями 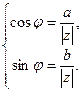
Доказательство. Если 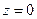 , то
, то 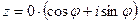 . Здесь
. Здесь 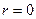 , а
, а 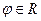 .
.
Если 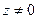 , то
, то 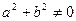 и
и 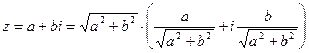 . Заметим, что
. Заметим, что 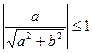 и
и 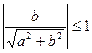 , а
, а 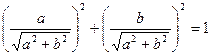 . Следовательно, существует такое, что
. Следовательно, существует такое, что 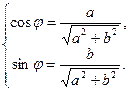 . Если обозначить
. Если обозначить 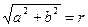 , то комплексное число
, то комплексное число 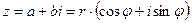 , причем r и
, причем r и 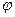 удовлетворяют условиям теоремы. Покажем теперь, что модуль комплексного числа находится однозначно, а аргумент – с точностью до слагаемого, кратного
удовлетворяют условиям теоремы. Покажем теперь, что модуль комплексного числа находится однозначно, а аргумент – с точностью до слагаемого, кратного 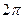 . Пусть
. Пусть 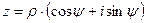 , где
, где 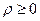 , а
, а 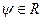 . Тогда
. Тогда 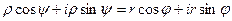 , откуда
, откуда 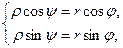 откуда
откуда 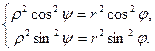 . Складывая эти равенства, получим
. Складывая эти равенства, получим 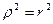 , или
, или 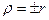 . Но так как оба числа положительны, то
. Но так как оба числа положительны, то 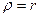 . Теперь систему можно преобразовать
. Теперь систему можно преобразовать 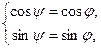 откуда, в силу периодичности косинуса и синуса, делаем вывод, что
откуда, в силу периодичности косинуса и синуса, делаем вывод, что 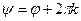 ■
■
Примеры. Записать каждое из чисел 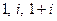 в тригонометрической форме записи. (Используя формулы перехода)
в тригонометрической форме записи. (Используя формулы перехода)
Далее установим геометрические свойства модуля и аргумента комплексного числа. Для этого сначала обратимся к рассмотренным примерам и изобразим данные комплексные числа на комплексной плоскости.
Итак, модуль ненулевого комплексного числа z есть расстояние от точки z на комплексной плоскости до начала координат, а аргумент – величина угла, образованного лучом Oz и положительным направлением действительной оси.
Примеры. Изобразить на комплексной плоскости множество точек, удовлетворяющих условиям: а) 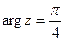 , б)
, б) 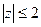 , в)
, в) 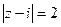 , г)
, г) 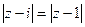 .
.
 2014-01-25
2014-01-25 1064
1064
