Статистические таблицы
Сущность и классификация статистических группировок
Понятие сводки статистических данных
ТЕМА 3. СВОДКА И ГРУППИРОВКА СТАТИСТИЧЕСКИХ ДАННЫХ
На основе информации, собранной в ходе статистического наблюдения, нельзя непосредственно выявить и охарактеризовать закономерности социально-экономических явлений, потому что наблюдение представляет сведения о каждой единице исследуемой совокупности. Эти данные не являются обобщающими показателями и с их помощью нельзя сделать выводы в целом об объекте исследования.
Сводка и группировка данных проводятся на втором этапе статистического исследования.
Сводкой в статистике называетсянаучно организованная обработка материалов наблюдения, включающая в себя кроме обязательного контроля собранных данных, систематизацию, группировку материалов, составление таблиц, получение итогов и производных показателей (средних, относительных величин).
Цель сводки – получение на основе сведенных материалов обобщающих статистических показателей, отражающих сущность социально-экономических явлений и определенные статистические закономерности.
Статистическая сводка осуществляется по программе, которая должна разрабатываться еще до сбора статистических данных, практически одновременно с составлением плана и программы статистического наблюдения. Программа сводки разрабатывается в соответствии с целью исследования и включает определение: групп и подгрупп;системы показателей;видов таблиц.
По глубине обработка данных сводка бывает простая и сложная. Простой сводкой называют операцию по подсчету общих итогов совокупности. Сложная сводка – комплекс операций, включающий группировку единиц наблюдения, подсчет итогов по каждой группе и по всему объекту в целом, а также представление результата группировки и сводки в виде статистической таблицы.
Группировка – это разбиение совокупности на группы, однородные по какому-либо признаку. С точки зрения отдельных единиц совокупности группировка – это объединение отдельных единиц совокупности в группы, однородные по каким-либо признакам.
Метод группировки основывается на двух понятиях - группировочном признаке и интервале.
Группировочный признак (или основание группировки) – это признак, по которому происходит объединение единиц совокупности в однородные группы.
Если разбиение элементов совокупности на группы осуществляется по атрибутивному признаку, то такой вид группировки называют классификацией.
Зависимые признаки называют результативными, а признаки, оказывающие влияние на них, - факторными. Следовательно, группировочный признак является обычно факторным, а характеризующий группировку – результативным.
Интервал очерчивает количественные границы групп, когда в основании группировки положен непрерывный количественный признак. Как правило, он представляет собой промежуток между максимальными и минимальными значениями признака в группе.
Интервалы бывают равные и неравные, открытые и закрытые.
Если разность между максимальным и минимальным значениями в каждом из интервалов одинакова, то интервалы будут равными. Если это условие не соблюдается, то – неравными. Открытые интервалы имеют только либо верхнюю, либо нижнюю границу, закрытые - и нижнюю, и верхнюю границы.
Количество образуемых групп зависит от размаха варьирования признака (разности между максимальным и минимальным его значениями).
Существуют различные математические методы определения числа групп. В частности, зависимость между числом формируемых групп (n) и численностью единиц совокупности (N) выражена в формуле американского ученого Стерджесса: n = 1 + 3,322 lgN. Эта зависимость может служить ориентировкой при определении числа групп в том случае, если распределение единиц совокупности по данному признаку приближается к нормальному и применяются равные интервалы в группах. На основании формулы Стерджесса составлена монограмма (см. табл. 3.1).
Таблица 3.1
Данные, характеризующие зависимость числа групп от численности совокупности
| N | 15-24 | 25-44 | 45-89 | 90-179 | 180-359 | 360-719 | 720-1439 |
| n |
Расчет величины интервала (i) при равных интервалах осуществляется по формуле:
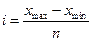 ,
,
где xmax и xmin – максимальная и минимальная величина признака группировки.
Полученную по формуле величину округляют, и она является шагом интервала (h).
Если основанием группировки служит непрерывный признак, то одно и то же значение признака выступает и верхней и нижней границами у двух смежных интервалов. Верхняя граница i -го интервала равна нижней (i + 1)-го. В данном случае нижнюю границу можно формировать по признаку включительно, а верхнюю исключительно или наоборот. Если в основании лежит дискретный признак, то нижняя граница i -го интервала равна верхней границе (i – 1)-го, увеличенной на 1.
Ширина открытого интервала принимается равной ширине смежного с ним интервала.
Характеристика разновидностей статистических группировок приведена в табл. 3.2.
Таблица 3.2.
Классификация статистических группировок
| Классификационный признак | Название группировок | Сущностная характеристика группировок |
| По целям группировки данных | Типологические | Решают задачу выделения качественно однородных совокупностей, а, именно, выявления и характеристики социально-экономических типов (классов, частных подсовокупностей) |
| Структурные | Преследуют цель изучения структуры совокупности - дают возможность описать составные части совокупности или строение типов, проанализировать структурные сдвиги | |
| Аналитические (факторные) | Нацелены на исследование существующих зависимостей - позволяет оценивать связи между взаимодействующими признаками социально-экономического явления | |
| В зависимости от числа положенных в основание группировки признаков | Простые (одномерные) | Проводятся по одному признаку |
| Многомерные | Проводятся по двум или нескольким признакам. Частый случай многомерной группировки - комбинационная группировка, базирующаяся на двух и более признаках, взятых во взаимосвязи, в комбинации | |
| По очередности обработки информации | Первичные | Составлены на основе первичных данных |
| Вторичные | Являются результатом перегруппировки ранее уже сгруппированного материала | |
| По отношениям между признаками | Иерархические | Выполняются по двум и более признакам, при этом значения второго признака определяется областью значений первого |
| Неиерархические | Строятся, когда строгой зависимости (подчиненности) значений второго признака от первого не существует |
Статистические таблицы являются средством наглядного выражения результатов исследования, они позволяют изолированные статистические данные рассматривать совместно, достаточно полно и точно охватывая сложную природу явлений. Это форма наиболее краткого и рационально изложения данных об изучаемой статистической совокупности.
Статистическая таблица – система строк и столбцов, в которых в определенной последовательности и связи излагается статистическая информация о социально-экономических явлениях.
Важное направление обработки статистических материалов - составление макетов таблиц, образец которого показан на рис. 3.1.
Таблица (номер)
 Название таблицы
Название таблицы

| |||||
| |||||

| |||||
| А | |||||
| |||||

| |||||
Рис. 3.1. Макет статистической таблицы
Различают подлежащее и сказуемое статистической таблицы.
Подлежащим таблицы называется объект, отдельные единицы или его части (группы), которые характеризуются соответствующими показателями. Сказуемым таблицы называются показатели, которые характеризуют подлежащее. Подлежащее таблицы обычно составляет название ее строк, сказуемое – название граф (колонок). Иногда в целях получения более компактной таблицы подлежащее и сказуемое меняют местами, т.е. подлежащее указывают по графам, а сказуемое по строкам.
По построению подлежащего таблицы могут быть: простыми, групповыми, комбинационными.
Простой называется такая статистическая таблица, в подлежащем которой нет группировок. Простые таблицы бывают: перечневые (подлежащее – перечень единиц, составляющих объект изучения); территориальные (дается перечень территорий, стран, областей, городов и пр.); хронологические (в подлежащем приводятся периоды времени или даты). Как правило, простые таблицы представляют данные в динамике.
Групповыми называются таблицы, в подлежащем которых изучаемый объект разделен на группы по какому-либо признаку. Такие таблицы, как правило, характеризуют в динамике состав и структуру изучаемого явления.
Комбинационной таблицей называется такая, где в подлежащем дана группировка единиц совокупности по двум и более признакам, взятым в комбинации. Пример комбинационной таблицы приведен посредством табл. 3.3
Таблицы различаются и по разработке сказуемого, которая может быть простой и сложной. Простая разработка сказуемого предусматривает параллельное расположение показателей, а сложная – комбинированное (в макете таблицы на рис. 3.1 это графы 3, 4, 5).
Основные правила построения таблиц
1. Таблица по возможности должна быть краткой. Не следует загружать ее излишними подробностями, затрудняющими анализ исследуемых явлений.
2. Каждая таблица должна иметь подробное название, из которого становится известно: а) какой круг вопросов излагает и иллюстрирует таблица; б) каковы географические границы статистической совокупности, представленные таблицей; в) каков период времени, за который приведены данные, или момент времени, к которому они относятся; г) каковы единицы измерения (если
Таблица 3.3
 2014-01-25
2014-01-25 769
769







