Показатели тесноты связи между двумя атрибутивными признаками

Общая характеристика таблиц взаимной сопряженности. Понятие корреляционной зависимости

ТЕМА 8. АНАЛИЗ ТАБЛИЦ ВЗАИМНОЙ СОПРЯЖЕННОСТИ

Общие понятия и схема статистической проверки гипотез

ТЕМА 7. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ

Оценку генерального параметра (какой-либо характеристики генеральной совокупности) получают на основе выборочного показателя с учетом ошибки репрезентативности. В другом случае в отношении свойств генеральной совокупности выдвигается некоторая гипотеза о величине средней, дисперсии, характере распределения, форме и тесноте связи между переменными. Проверка гипотезы осуществляется на основе выявления согласованности эмпирических (полученных опытным путем) данных с гипотетическими (теоретическими). Если расхождения между сравниваемыми величинами не выходит за пределы случайных ошибок, гипотезу принимают. При этом не делается никаких заключений о правильности самой гипотезы, речь идет лишь о согласованности сравниваемых данных. Основой проверки статистических гипотез являются данные случайных выборок.

Статистической гипотезой называется предположение о свойстве генеральной совокупности, которое можно проверить, опираясь на данные выборки.

Обозначается гипотеза буквой H от латинского слова hypothesis. При записи содержание гипотезы отделяется от символа Н двоеточием. Например, может быть выдвинута гипотеза о том, что средняя в генеральной совокупности больше некоторой величины, Н: 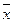> b.

Различают простые и сложные гипотезы.

Гипотеза называется простой, если она однозначно характеризует параметр распределения случайной величины. Например, Н: 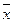= b.

Сложная гипотеза состоит из конечного или бесконечного числа простых гипотез, при этом указывается некоторая область вероятных значений параметра. Например, Н: 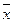> b. Эта гипотеза состоит из множества простых гипотез Н: 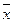= с, где с – любое число, большее b.

Проверяемая гипотеза называется основной (нулевой) и обозначается Н_о. Суть проверки – убедиться в отсутствии систематической ошибки между исследуемым параметром генеральной совокупности и заданным его значением, т.е. проверяется гипотеза о нулевом расхождении между ними. Например, выдвигается гипотеза о том, что две совокупностим, сравниваемые по одному или нескольким признакам, не отличаются. При этом предполагается, что действительное различие сравниваемых величин равно нулю, а выявленное по данным отличие от нуля носит случайный характер. Н_о: 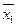=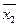и т.п.

Нулевая гипотеза отвергается тогда, когда по выборке получается результат, который при истинности выдвинутой нулевой гипотезы маловероятен.

Альтернативная гипотеза Н₁ может быть сформирована по разному в зависимости от того, какие отклонения от гипотетической величины нас особенно беспокоят: положительные, отрицательные, либо и те и другие. Соответственно альтернативные гипотезы могут быть записаны как

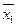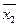Н₁: 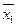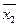>, Н₁: <, Н₁: ≠.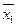

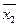От того, как формируется альтернативная гипотеза, зависят границы критической области и области допустимых значений.

Поскольку при проверке гипотезы используются данные выборочного наблюдения, вывод о ее допустимости носит вероятный характер, т.е. не исключена возможность ошибки. При этом могут возникать следующие ошибки:

- ошибка первого рода – если в результате проверки делается вывод о необходимости отклонить нулевую гипотезу, которая в действительности верна (неправильное отклонение нулевой гипотезы);

- ошибка второго рода – если нулевая гипотеза не отклоняется, хотя на самом деле она ошибочна (неправильное принятие нулевой гипотезы).

Для того чтобы сделать вывод о соответствии результатов выборочного наблюдения выдвинутой гипотезе, необходимо принять определенный критерий.

Статистическим критерием называют правило определяющее условия, при которых проверяемую нулевую гипотезу следует либо отклонить, либо не отклонить. Критерий проверки статистической гипотезы определяет, противоречит ли выдвинутая гипотеза фактическим данным или нет. Например, при проверке гипотезы о среднем значении признака в генеральной совокупности Н_о: 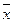= а в качестве критерия (θ) можно использовать среднее значение признака в выборке .

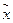Из множества значений статистического критерия необходимо выделить такое их подмножество, при попадании в которое выборочной характеристики основная гипотеза должна быть отклонена как противоречащая фактическим данным. Это подмножество называется критической областью.

Критической областью называется область, попадание значения статистического критерия в которую приводит к отклонению Н_о. Ее границы устанавливаются таким образом, чтобы вероятности попадания в нее значений выборочной характеристики при условии справедливости выдвинутой гипотезы была достаточно малой. Напомним, что указанная вероятность называется уровнем значимости критерия α. Обычно уровень значимости принимается равным 0,05; 0,01; 0,005; 0,001. Если нулевая гипотеза верна, то вероятность ее принятия равна (1 – α).

Область допустимых значений дополняет критическую область. Если значение критерия попадает в область допустимых значений, это свидетельствует о том, что выдвинутая гипотеза Н_о не противоречит фактическим данным (Н_о не отклоняется).

Точки, разделяющие критическую область и область допустимых значений, называются критическими точками или границами критической области. В зависимости от формулировки альтернативной гипотезы критическая область может быть двухсторонняя или односторонняя (левосторонняя либо правосторонняя). Например, при Н_о: 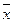= а, альтернативные гипотезы могут быть представлены как: Н₁: 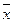≠ а; Н₁: 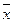< а; Н₁: 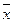> а.

Проверка статистических гипотез предполагает последовательную реализацию действий, приведенных на рис. 7.1.

Рис. 7.1. Основные этапы проверки статистических гипотез

В зависимости от вида проверяемых гипотез (о среднем значении, законе распределения, взаимосвязи признаков и т.д.) выбираются разные критерии (t -статистика (или коэффициент доверия), t -статистика Стьюдента, χ² -критерий Пирсона (хи-квадрат), F -критерий Фишера и др.).

Наличие зависимости между показателями, характеризующими статистическую совокупность, можно выявить с помощью аналитической группировки.

Результаты группировки единиц совокупности могут быть оформлены в виде таблицы, в которой приведено комбинационное распределение единиц совокупности по двум признакам. Такие таблицы называют таблицами взаимной сопряженности.

Если в таблице оба признака, по которым дано распределение единиц совокупности, количественные, то такая таблица взаимной сопряженности называется корреляционной.

Слово «корреляция» (от английского correlation) означает соотношение, соответствие. Оно удачно отражает особенность зависимости, при которой определенному значению одного факторного признака может соответствовать несколько значений результативного признака (показателя). На основе этих значений можно определить среднюю величину последнего, соответствующую каждому конкретному значению факторного признака.

Связь, при которой разным значениям факторного признака соответствуют различные средние значения результативного признака называется корреляционной. Именно корреляционные связи наиболее часто используются при исследовании общественных явлений.

Суть корреляционной зависимости сводится к тому, что, с изменением значения признака х закономерным образом изменяется среднее значение признака у, в то время как в каждом отдельном случае значение признака у (с различными вероятностями) может принимать множество различных значений.

По направлению различают прямые и обратные связи. При прямой связи с ростом факторного признака растет и результативный признак. При обратной связи с увеличением факторного признака результативный уменьшается или наоборот. Например, рост производительности труда приводит к снижению себестоимости единицы продукции.

Корреляционная таблица строится по типу «шахматной», т.е. в подлежащем таблицы выделяются группы по факторному признаку х, в сказуемом – по результативному у или наоборот, а в клетках таблицы на пересечении х и у показано число случаев совпадения каждого значения х с соответствующим значением у. Макет корреляционной таблицы показан с помощью табл. 8.1.

Таблица 8.1

Корреляционная таблица

Значение признака xi	Значение признака yj	Итого (число единиц) fx = fj	Среднее значение по группам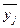
y1	y2	…	ym
x1 x2 … xn					f1 f2 … fn
Итого (число единиц) fy = fi	f1	f2	…	fm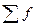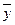

Корреляционная связь существует, если по мере увеличения значения х групповые средние значений у тоже увеличиваются (или уменьшаются) от группы к группе.

О наличии и направлении связи можно судить и по «внешнему виду» таблицы, т.е. по расположению в ней частот.

Так, если числа (частоты) расположены (разбросаны) в клетках таблицы беспорядочно, то это чаще всего свидетельствует либо об отсутствии связи между группировочными признаками, либо об их незначительной зависимости.

Если же частоты сконцентрированы ближе к одной из диагоналей и центру таблицы, образуя своего рода эллипс, то это почти всегда свидетельствует о наличии зависимости между х и у, близкой к линейной. Диагональ из верхнего левого угла в нижний правый свидетельствует о прямой линейной зависимости между показателями х и у, а из нижнего левого угла в верхний правый – об обратной.

Наглядно проиллюстрировать наличие и форму зависимости между показателями х и у по данным корреляционной таблицы можно и графически. Отметим, что установление формы зависимости между показателями, определение функции регрессии (уравнения связи) и т.п. являются задачами регрессионного анализа.

При построении эмпирической линии регрессии по данным корреляционной таблицы на графике по оси абсцисс отражают значения факторного признака (или середины соответствующих интервалов) х, а по оси ординат – групповые средние результативного показателя, т.е. 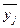. Для большей наглядности на графике по исходным данным можно построить «корреляционное поле», а затем на его фоне - эмпирическую линию регрессии.

Корреляционное поле представляет, по существу, ту же корреляционную таблицу, в клетках которой вместо чисел проставлено соответствующее число точек. Корреляционное поле отражает не только общую зависимость между х и у, но и концентрацию индивидуальных точек вокруг линии регрессии показателя 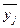. На рис. 8.1 показаны варианты распределения корреляционного поля.

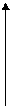
У У У

а) Х б) Х в) Х

Рис. 8.1. Распределение корреляционного поля при разных видах зависимости

Если точки расположены хаотично по всему полю, то это свидетельствует об отсутствии зависимости между двумя признаками (рис. 8.1, а), если они сконцентрированы около оси, идущей от нижнего левого угла к верхнему правому (рис. 8.1, б), – это прямая зависимость между исследуемыми признаками; если точки будут сконцентрированы около оси, пролегающей от верхнего левого угла к нижнему правому (рис. 8.1, в)– имеет место обратная зависимость.

На основе аналитических группировок и корреляционных таблиц можно не только выявить наличие зависимости между двумя коррелируемыми показателями, но и измерить тесноту этой связи, в частности, с помощью эмпирического корреляционного отношения (см. п. 5.5).

,

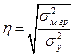где 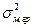и 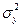- соответственно межгрупповая и общая дисперсии результативного признака, рассчитываемые как

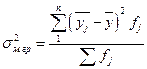и ,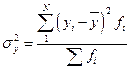

где n – число групп по факторному признаку х;

N – число единиц совокупности;

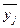- среднее значение результативного признака по группам;

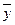- общее среднее значение результативного признака;

y_i – индивидуальные значения результативного признака;

f_j = f_x – частота в j -й группе х;

f_i = f_y – частота в i -й группе у.

Построение таблиц, в которых дается комбинационное распределение единиц совокупности по двум признакам применимо и к атрибутивным признакам. Взаимосвязи между атрибутивными признаками, их влияние на другие показатели, в том числе и количественные, особенно часто приходится изучать при проведении различных социологических исследований.

Простейшей формой таблицы взаимной сопряженности двух атрибутивных признаков является таблица «четырех полей» (четырехклеточная). В ней по каждому признаку выделяются только две группы, чаще всего по альтернативному принципу («да»-«нет», «хорошо»-«плохо» и т.д.)

Для измерения тесноты связи между двумя атрибутивными признаками, имеющими альтернативное выражение, используется коэффициент ассоциации, рассчитываемый с помощью таблицы взаимной сопряженности, которая состоит из четырех клеток, обозначенных латинскими буквами a, b, c, d. Каждая клетка соответствует определенной альтернативе того или иного признака (табл. 8.2).

Таблица 8.2

Таблица взаимной сопряженности двух атрибутивных признаков

Признак	А	не А	∑ В
В	a	b	а + b
не В	c	d	c + d
∑ А	a + c	b + d	a + b + c + d

Коэффициент ассоциации (К_асс) определяется по формуле: .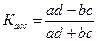

Его существенный недостаток состоит в том, что если в одной из четырех клеток отсутствует частота (т.е. равна 0), коэффициент ассоциации всегда будет равен по модулю 1, и тем самым преувеличена мера действительной связи.

Чтобы этого избежать, предложен другой показатель – коэффициент контингенции (К_конт):

.

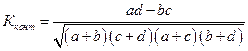Коэффициент контингенции всегда меньше коэффициента ассоциации.

Связь считается достаточно значительной и подтвержденной, если | К_асс |>0,5 или | К_конт |>0,3.

Для исследования корреляции атрибутивных альтернативных признаков предложен также

коэффициент колигации (К_кол):.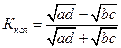

Коэффициент колигации, как и коэффициент контингенции, оценивают связь между признаками более сдержанно, чем коэффициент ассоциации, причем всегда: К_асс > К_кол > К_конт.

В том случае, когда оба взаимосвязанных признака разделены более чем на две группы, то для измерения тесноты связи используются показатели взаимного сочетания (сопряжения), предложенные Пирсоном и Чупровым.

Коэффициент взаимной сопряженности Пирсона: ,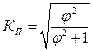

где φ (греческая буква «фи») – показатель средней квадратической сопряженности, определяемый путем вычитания единицы из суммы отношений квадратов частот каждой клетки корреляционной таблицы к произведению частот соответствующего столбца и строки:

, , .

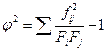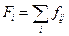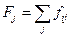Коэффициент взаимной сопряженности Чупрова: ,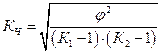

где К₁ – количество групп в графах;

К₂ – количество групп в строках.

Результат, полученный по коэффициенту взаимной сопряженности Чупрова, более точен, поскольку он учитывает количество групп по каждому из исследуемых признаков. Его выгодно использовать и при большем разделении единиц совокупности на группы по взаимосвязанным признакам. Коэффициент взаимной сопряженности Пирсона используется в основном в случае квадратичной таблицы, тогда как Чупрова – пригоден для измерения связи и в прямоугольных таблицах.

Считается, что уже при значении коэффициентов взаимной сопряженности 0,3 можно говорить о тесной связи между вариацией исследуемых признаков.