Статистические группировки, при помощи которых выявляют взаимосвязи между признаками общественных явлений, называются аналитическими.
Метод статистических группировок как способ выявления корреляционной зависимости относится к числу наиболее важных методов исследования взаимосвязей. Напомним, что для выявления зависимости между признаками при помощи этого метода материал статистического наблюдения группируется по факторному признаку, и для каждой группы рассчитываются средние значения как факторного, так и результативного признака. Сравнивая изменения средних значений результативного признака с изменениями средних значений факторного признака, выявляют характер связи между ними.
Группировка позволяет также выявить одновременное влияние нескольких факторов на результативный признак. Для этого проводят комбинационные группировки, их данные заносятся в комбинационные таблицы.
Аналитические группировки характеризуют только общие черты исследуемой связи, ее тенденцию, однако не дают количественной оценки силы связи. На основе аналитических группировок эта задача решается при помощи расчета эмпирического корреляционного отношения (см. п. 8.1). Сущностная характеристика эмпирического коэффициента детерминации и эмпирического корреляционного отношения приведена в п. 5.5.
Следует отметить, что η > 0 не является доказательством наличия корреляционной связи между признаками. Отличное от нуля корреляционное отношение может появиться при неправильном распределении исследуемой совокупности на группы.
Проверка истинности причин отклонений групповых средних от общей средней осуществляется при помощи критериев, разработанных математической статистикой.
Эмпирическое корреляционное отношение должно иметь высокий уровень надежности.
Для оценки надежности корреляционных характеристик используют критерий Фишера (F - критерий) или Стьюдента (t - критерий).
Критерий Фишера определяется по формуле: 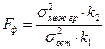 ,
,
где σ2ост – остаточная (средняя из внутригрупповых) дисперсия;
k1, k2 – степени свободы для межгрупповой и средней из внутригрупповых дисперсий.
Фишер установил распределение отношений дисперсий и разработал соответствующие математические таблицы. В них приводится F –критерий теоретический (Fт) при двух вероятностях 0,95 и 0,99. Если Fф > Fт, то с принятой степенью вероятности можно утверждать о наличии влияния исследуемого фактора на результативный признак. Если же Fф ≤ Fт, можно утверждать, что разница между дисперсиями обусловлена влиянием случайных факторов.
Распределение в таблицах Фишера для поиска Fт зависит от ступеней свободы k1 и k2 дисперсий. В аналитической группировки они рассчитываются по формулам:
k1 = m – 1; k2 = n – m,
где n – количество элементов исследуемой совокупности;
m – число групп.
К аналогичному выводу можно прийти при оценке надежности корреляционного отношения по критерию Стьюдента, который определяется по формуле:
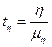 ,
,
где μη - средняя ошибка корреляционного отношения: 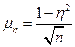 .
.
Если критерий Стьюдента tη ≥ 3, показатель корреляционного отношения считают вероятным (т.е. связь между исследуемыми явлениями доказана). Если tη < 3, то нельзя делать выводы о вероятности связи между исследуемыми явлениями.
Убедившись при помощи аналитической группировки и расчета показателя эмпирического корреляционного отношения, что теснота связи между исследуемыми явлениями достаточна высока, можно и перейти к корреляционно – регрессионному анализу.
 2014-01-25
2014-01-25 1288
1288
