Разрабатывая программу выборочного наблюдения, сразу задают величину допустимой ошибки выборки и доверительную вероятность. Неизвестным остается тот минимальный объем выборки, который должен обеспечить требуемую точность. Формулы для определения численности выборки (n) в зависимости от метода отбора для средней и доли приведены в табл. 6.4. Они следуют из формул предельных ошибок выборки.
Таблица 6.4
Численность выборки при собственно случайном и механическом отборе
| Метод отбора | Объем выборки, позволяющий обеспечить требуемую точность | |
| для средней | для доли | |
| Повторный | 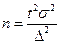
| 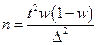
|
| Бесповторный | 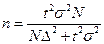
| 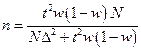
|
Значения ∆ и t определяются как задачами, стоящими перед исследователем, так и природой изучаемого явления. Чем более достоверные результаты требуется получить, тем большую вероятность необходимо задать. С увеличением допустимой ошибки уменьшается необходимый объем выборки, и наоборот. Например, увеличение ошибки выборки в 2 раза уменьшит n в 4 раза.
Вариация (σ2) признака существует объективно, независимо от исследователя, но к началу выборочного наблюдения она неизвестна. Приближенно σ2 определяют следующими способами:
1) берут из предыдущих исследований;
2) исходя из того, что общий размах вариации укладывается в 6 сигм (R ≈ 6 σ), σ ≈ R /6. Для большей точности R делят на 5;
3) если хотя бы приблизительно известна средняя величина изучаемого признака, то σ ≈ 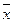 /3;
/3;
4) если известна дисперсия признака в генеральной совокупности, то 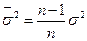 , если n – велико, то сомножитель (n -1)/ n ≈1 и можно принять выборочную дисперсию в качестве оценки генеральной дисперсии, и наоборот.
, если n – велико, то сомножитель (n -1)/ n ≈1 и можно принять выборочную дисперсию в качестве оценки генеральной дисперсии, и наоборот.
При стратифицированном отборе, не пропорциональном объему групп, общее число отбираемых единиц делится на количество групп. Полученная величина даст объем выборки из каждой группы.
При стратифицированном отборе, пропорциональном числу единиц в группе, число наблюдений по каждой группе определяется формулой
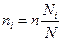 ,
,
где ni – объем выборки из i -й группы;
n – общий объем выборки;
Ni – объем i -й группы;
N – объем генеральной совокупности.
При серийном (гнездовом) отборе необходимую численность отбираемых серий определяют так же, как и при собственно случайном, только вместо N, n, σ2 подставляют R, r и σ2м. гр, где R – число серий в генеральной совокупности; r – число отобранных серий; σ2м. гр – межсерийная (межгрупповая) дисперсия.
 2014-01-25
2014-01-25 854
854








