Корреляционно-регрессионный анализ: аналитическое выражение уравнения (прямолинейной, криволинейной) регрессии для однофакторной корреляционно-регрессионной модели

Применение корреляционно-регрессионного метода анализа явлений начнем с оценки парной корреляции и построения однофакторной модели зависимости результативного признака от факторного в виде уравнения корреляционной связи. Уравнение корреляционной связи часто называют уравнением регрессии, показывающим вид зависимости среднего значения результативного признака от факторного. Аналитическая связь между результативным и факторным признаками может описываться уравнениями:

прямой 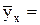a₀ + a₁x;

гиперболы 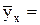a₀ + a₁/x;

параболы 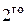порядка 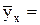a₀ + a₁x +a₂x²;

степенной функции 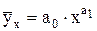и т.д.

Прежде чем приступить к построению модели – уравнения регрессии, необходимо выбрать тип функции, т.е. форму корреляционной связи. Некоторые данные о форме связи можно получить из графика эмпирической линии регрессии. Если на корреляционном поле соединить точки отрезками прямой, то получится ломаная линия с некоторой тенденцией к росту или снижению, которая и называется эмпирической линией регрессии. На рис. 8.2 представлена в качестве примера эмпирическая линия регрессии заработной платы почтовых работников (У) от их производительности труда (Х).

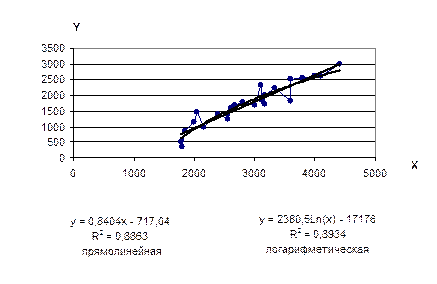
Рис. 8. 2. График корреляционной зависимости заработной платы (y)

и производительности труда (x). Графический способ подбора лучшей формы корреляционной зависимости между (y) и (x) по максимальному значению R².

Изломы эмпирической линии регрессии y обусловлены тем, что на результативный показатель оказывают влияние кроме х другие факторы. Если отвлечься (абстрагироваться) от влияния других факторов, кроме х, то можно сделать вывод о виде аналитической функции y_x, в определенной степени отражающей характер зависимости между y и х. В данном случае можно склониться к прямолинейной форме связи. Внешний вид эмпирической линии регрессии позволяет зрительно установить теоретическую форму зависимости y от х.

Главной же в обосновании формы теоретической линии связи должна быть экономическая теория, определяющая сущность и природу изучаемых явлений и, следовательно, взаимосвязь между ними. В примере взаимосвязь между оплатой труда и выработкой в виде прямой линии может быть принята только условно, для каких-то узких целей. В соответствии с экономической теорией воспроизводства, рост производительности труда должен опережать рост зарплаты, т.е. зависимость должна быть криволинейной и иметь вид экспоненты. При таком подходе к выбору зависимости корреляционное уравнение может быть использовано не только для анализа состояния экономической системы, но и для прогнозирования и планирования результатов и факторов производства.

После выбора вида зависимости приступают к расчету параметров аналитического уравнения корреляционной связи (уравнения регрессии). Параметры находят на основе метода наименьших квадратов. Для нахождения параметров уравнения прямой 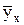= а₀+а₁х используется система нормальных уравнений вида:

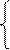a₀n+a₁Sx=Sy,

a₀Sx+a₁Sx²=Sxy,

где n – объем исследуемой совокупности (число единиц наблюдения).

Решение этой системы относительно а₀ и а₁ позволяет определить параметры уравнения регрессии:

; .

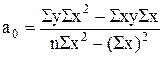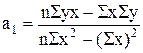По уравнению регрессии можно найти выровненные теоретические значения результативного признака при соответствующих значениях фактора х. Отклонения фактических значений (y) от теоретических 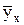обусловлены тем, что регрессия (y) строилась только по одному фактору (х), в то время как в действительности (y) зависит от множества факторов.

Выбор теоретической формы корреляционной связи всегда несколько условен, так как в действительности зависимости между признаками лишь приблизительно соответствуют функциональным. Поэтому только при высокой тесноте связи между признаками линия регрессии имеет содержательный смысл и практическое значение.

Показателями тесноты корреляционной связи служат коэффициент и индекс корреляции. Теснота связи между признаками измеряется с помощью показателей вариации результативного признака y.

На рис. 8.3 изображены три линии: y – ломаная, называемая эмпирической линией регрессии, которая отражает фактические значения y при соответствующих значениях факторного признака х; 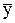– прямая линия, параллельная оси абсцисс, соответствующая среднему значению y при исключении влияния всех факторов; 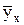– выравненная линия регрессии, характеризующая значения y при абстрагировании всех факторов, кроме фактора х. Поскольку на y помимо х оказывают влияние и другие факторы, то линия y не совпадает с линией 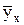. Это несовпадение свидетельствует о неполной связи между y и х.

Чтобы измерить, насколько связь близка к функциональной, исчисляют показатели тесноты связи. Для этого необходимо оценить вариацию результативного признака y, вызванную только влиянием признака х, и остаточную его вариацию, обусловленную прочими факторами.

Общая дисперсия результативного признака 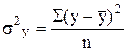характеризует вариацию y под влиянием всех факторов.

Средний квадрат отклонений 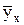от 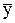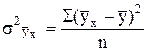измеряет вариацию y только под влиянием фактора х – это факторная дисперсия.

Средний квадрат отклонений y от 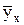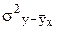= S(y–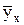)²/n характеризует остаточную вариацию y под влиянием всех остальных факторов. В математической статистике доказано, что s²_y = 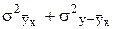, т.е. 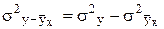. Поэтому эту дисперсию называют остаточной дисперсией, она характеризует вариацию y за счет остальных факторов, не включенных в уравнение регрессии.