Тема 8 Статистические методы изучения взаимосвязи между явлениями. Корреляционно-регрессионный анализ

Методы выявления тенденций (метод аналитического выравнивания). Выравнивание динамических рядов с сезонными колебаниями нагрузки. Выбор наилучшей аппроксимирующей зависимости. Понятие экстраполяции, интерполяции. Прогнозирование в заданном интервале.

Для отображения тенденции в развитии явлений важное место занимает способ аналитического выравнивания рядов динамики. При этом способе общее направление в развитии явления выражается плавно изменяющейся линией – трендом, характеризующим тенденцию его динамики. Аналитическая формула этой линии устанавливается математическими методами, при этом выбор формы кривой должен быть обоснован теоретическим анализом сущности данного явления и законов его развития.

Выравнивание может быть произведено по прямой или криволинейной зависимости, выражающей функциональную зависимость уровней ряда динамики от времени: 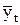= f(t).

Если явление развивается в арифметической прогрессии, т.е. цепные абсолютные приросты относительно стабильны: D_i = const, то в качестве тренда берется прямая линия – линейная функция вида 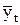= a₀+a₁t.

Если относительно стабильными являются цепные темпы прироста, т.е. уровни ряда растут с какой-то постоянной скоростью, то в качестве тренда принимается экспонента (показательная функция) вида 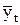= a₀a₁^t.

При равномерном увеличении (уменьшении) цепных абсолютных приростов, т.е. монотонном изменении уровней ряда с возрастающей (убывающей) скоростью, в качестве аппроксимирующей функции принимается полином второй степени – парабола второго порядка 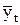= a₀+a₁t+a₂t².

При моделировании динамических рядов, в которых наблюдается быстрое развитие в начале ряда и затухающее его развитие к концу, т.е. стремление к некоторой предельной величине, применяются логистическая функция вида 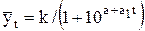. При наличии экстремальных значений ряд динамики описывается кривой Гомперца .

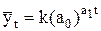В приведенных уравнениях 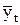– значение уровня выравненного ряда; а₀ и а₁ – параметры уравнения; t – показатель времени (дни, месяцы, годы). В статистической практике параметры уравнений интерпретируются следующим образом: a₀ – характеризует средние условия ряда динамики, а₁ – изменение скорости (ускорения), в линейной функции показывает, на сколько изменится уровень ряда при изменении единицы времени на единицу.

Задача аналитического выравнивания сводится к тому, чтобы фактические значения ряда динамики Y заменить теоретическими Y_t, исчисленными на основании уравнения. Параметры уравнений находят различными методами: конечных разностей, наименьших квадратов, гармонического анализа. Для нахождения параметров уравнений методом наименьших квадратов решается система нормальных уравнений. Для уравнения прямой строится следующая система уравнений:

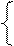a₀n + a₁St = Sy,

a₀St + a₁St² = Syt,

где n – число членов ряда; t – показатель времени, обозначаемый порядковыми номерами, начиная с низшего, например: t = 1, 2, 3, 4...

Решение системы нормальных уравнений позволяет получить выражение для параметров a₀ и a₁: ; .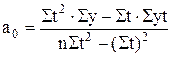

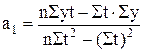Так как в рядах динамики значения t являются показателями времени, то всегда можно им придать такое значение, чтобы их сумма была равна нулю, т.е. St=0. В этом случае система нормальных уравнений принимает вид

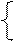Sy = a₀n,

Syt = a₁St²,

расчет параметров упрощается: a₀=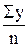, a₁=.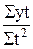

Для определения параметров показательной функции 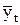= a₀a^t₁ сначала по методу наименьших квадратов логарифмируют уровни ряда, по системе нормальных уравнений находят логарифмы а₀ и а₁, которые затем потенцированием приводят к нормальному виду: lg a₀ = 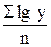; lg a₁ = 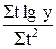(при St=0).

Параметры параболы второго порядка исчисляют следующим образом (при St=0): а₁ = 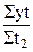; параметры а₀ и а₂ находят решением системы:

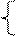a₀n + a₂St² = Sy,

a₀St² + a₂St⁴ = Syt².

Наилучшую аппроксимирующую функцию выбирают по размеру

стандартной ошибки: S = 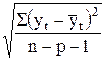(где p – число параметров уравнения) или минимуму остаточной дисперсии: s²_ост = S(y_t–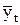)²/n.

Статистическая практика анализа рядов динамики в отрасли показывает, что для:

- выравнивания экономических показателей деятельности организаций, подотраслей и отрасли связи в целом в наибольшей мере подходят уравнения прямой, параболы второго порядка и экспоненты;

- прогнозирования результатов научно-технического прогресса, спроса и предложения новых услуг, средств связи – показательная и логистическая функции.

При анализе изменения объема услуг по месяцам года, дням недели, часам суток содержатся заметные периодические колебания вокруг общей тенденции, т.е. цикличность в изменении их уровней. Закономерность в колебаниях уровней ряда динамики характеризуется периодической компонентой, которая выявляется с помощью гармонического анализа.

Неравномерность спроса и поступления нагрузки в организациях связи оказывает серьезное влияние на предложения услуг, режим работы, использование средств связи, рабочей силы и резервирование производственных мощностей для передачи информации в часы наибольшей нагрузки (ЧНН). Задача статистики связи – выявить и измерить неравномерность нагрузки.

Внутригодовые колебания, имеющие более или менее регулярный характер, представляют собой сезонную компоненту ряда динамики. Закономерности в изменении уровней ряда динамики по месяцам года называются сезонными колебаниями. Мерой сезонных колебаний являются индексы сезонности I_S.

Индексы сезонности I_S являются мерой сезонных колебаний объема услуг связи, определяются отношением объема услуг за месяц к среднемесячному объему услуг за год: I_S = y_i100/ 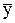, где y_i – объем услуг за i-тый месяц; 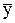– среднемесячный объем услуг за год; 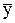= Sy_i/12. Совокупность индексов сезонности I_S за один год или несколько лет образует сезонную волну. В практической деятельности организаций связи индексы сезонности по аналогии с коэффициентами суточной и часовой неравномерности называют коэффициентами месячной неравномерности, показывающими, во сколько раз нагрузка данного месяца больше или меньше среднемесячной нагрузки за год. Средние индексы сезонности рассчитывают двумя способами: на основании месячных индексов сезонности за ряд лет либо абсолютных данных о месячном объеме услуг за все эти годы. Для её оценки применяют различные методы:

1) если изменения ряда имеют определенную тенденцию, то вычисляют сезонную волну фактических уровней ряда y_i по отношению к выравненным по какой-либо функции 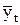(уравнению прямой, синусоиды или ряду Фурье): I_s = y_i100/;

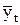2) если ряд не содержит ярко выраженной тенденции, то индексы сезонности рассчитывают по эмпирическим данным без предварительного выравнивания по формуле, соответствующей расчету коэффициентов месячной неравномерности: I_s = y_i100/.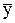

В рядах с тенденцией сезонных колебаний производят аналитическое выравнивание по:

· синусоиде 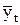= A∙sin(at+b), где t – период колебательного движения (длина волны t = p/a); A – полуамплитуда колебания, т.е. наибольшее и наименьшее отклонение от оси t; b – начальная фаза колебания. При St = 0 синусоида имеет вид 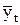= A∙sin b;

· ряду Фурье ,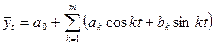

где t – период времени (месяц, год); k – номер гармоники ряда Фурье, т.е. число синусоид, k = 1...m.

Параметры ряда Фурье при одной синусоиде (k = 1) и St = 0 находятся следующим образом: a₀ = 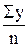; a = 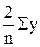cos t; b = 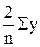sin t, где n – количество месяцев (лет).

Если все колебания членов ряда объясняются сезонными причинами (например, изменения количества посылок определяются временем созревания овощей и фруктов), то при равенстве среднего индекса сезонности 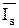= 100% ( 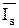= SI_si/n) уравнение тренда выражают только сезонные колебания нагрузки. Это дает основание использовать полученную аналитическую функцию для планирования производственных мощностей и расстановки кадров в будущем периоде. Поэтому наилучшее с точки зрения отражения сезонных колебаний нагрузки уравнение выбирают по минимуму среднего квадратического отклонения индексов сезонности от 100%:

s = .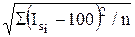

В тех случаях, когда в рядах динамики отсутствуют некоторые данные, прибегают к интерполяции, т.е. определению неизвестных уровней внутри данного ряда.При прогнозировании уровней ряда в будущем при предположении сохранения закономерности развития, действующей в прошлом, используется экстраполяция.

При интерпретации считается, что ни выявленная тенденция, ни её характер не претерпели существенных изменений в том промежутке времени, уровень которого не известен.

Применение экстраполяции в прогнозировании базируется на следующих предпосылках:

- развитие исследуемого явления в целом следует описывать плавной кривой;

- общая тенденция развития явления в прошлом и настоящем не должна претерпевать серьёзных изменений в будущем. Экстраполяция, проводимая в будущее, называется перспективной, а в прошлое – ретроспективной.

Экстраполяция в общем виде можно представить формулой: ,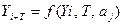

где 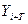- прогнозируемый уровень, 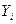- текущий уровень, Т –период упреждения, 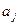- параметр уравнения тренда.

Любой статистический прогноз носит приближенный характер, поэтому целесообразно определять доверительные интервалы к прогнозируемому значению уровня: 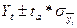или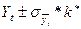

где 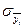- средняя квадратическая ошибка тренда, 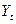- расчетное значение уровня,

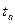- доверительная величина. Вместо 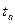-критерия Е.М. Четыркин предлагает брать коэффициенты (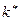), которые приведены в его книге (Е.М. Четыркин Статистические методы прогнозирования. – М.: Статистика, 1975.).

Статистические методы, реализованные в системе STATISTICA, позволяют построить объективный прогноз данных с вычислением нижних и верхних границ доверительных интервалов с определенной вероятностью (75,90,95%).