Статистическое изучение взаимосвязи между явлениями: практическое применение, понятие факторного и результативного признаков. Виды связей (функциональные, стохастические). Понятие корреляционной связи, условия её возникновения. Методы исследования функциональных связей между явлениями.
Теоретический анализ сущности социально-экономических явлений и вскрытие причинно-следственных отношений позволяют разграничить взаимосвязанные признаки на факторные (независимые), которые изменяются независимо от других, и результативные (зависимые), значение которых обусловлено воздействием и изменениями факторных.
Отнесение того или иного признака к результативному или факторному определяется экономической сущностью явлений и задачей исследования. Например, класс квалификации, уровень автоматизации производственных процессов, стаж работы, тип аппаратуры связи – это факторы, влияющие на производительность труда работников связи, являющуюся результатом воздействия этих признаков. В то же время производительность труда может являться факторным признаком при анализе себестоимости услуг связи, рентабельности производства.
При изучении взаимосвязей между явлениями встречаются с функциональными (полными) и стохастическими (неполными) связями. При функциональной связи значение результативного признака однозначно определяется значениями факторных признаков. При этом результативный признак принимает строго определенное значение, которое можно рассчитать по формуле, выражающей эту функциональную связь. К функциональным зависимостям можно отнести формулы для расчета тех или иных экономических показателей. Например, производительность труда есть частное от деления доходов от реализации услуг продукции на численность работников W=Д/T, себестоимость услуг определяется делением затрат на производство услуг на их объем в натуральном выражении с=Э/q и т.д.
В действительности взаимосвязи в социально-экономических явлениях значительно сложнее, они транзитивны, многофакторны и не носят функционального характера. Так, производительность труда определяется не просто величиной доходов от реализации услуг и численностью работников, а, в первую очередь, уровнем организации производства и маркетинговой деятельности, степенью прогрессивности оборудования, автоматизации труда, сбалансированной тарифной политикой; каждая из этих причин в свою очередь также многофакторна.
Изучая массовые данные о каком-либо общественном явлении, всегда можно видеть множество случаев, когда одному и тому же значению результативного признака могут соответствовать различные значения факторов и наоборот.
Перечислить все факторы, влияющие на изучаемые явления, невозможно; тем более невозможно создать окончательную или общую для всех случаев формулу, устанавливающую взаимосвязь между результативным и факторным показателями.
Для характеристики реальных взаимосвязей, проявляющихся в общем, среднем, при большом числе наблюдения, статистика прибегает к изучению стохастических зависимостей, частным случаем которых, является корреляционная связь. Корреляционной называется такая связь, которая проявляется только в среднем, когда каждому значению факторов соответствует среднее значение результативного показателя. "Корреляция" в переводе с позднелатинского (correlatio) означает "соотношение", "соответствие", "взаимосвязь", "взаимозависимость". Она заключается в том, что изменение среднего значения результативного признака обусловлено изменением значений факторных признаков.
Корреляционные связи проявляются при достаточно большом числе наблюдений. Только в массе достигается устойчивость средних величин, что обусловлено действием закона больших чисел. Корреляционные связи – это неполные связи, поскольку результативный признак зависит еще от множества факторов, не учтенных уравнением корреляционной связи. Корреляционные связи в общественных и социально-экономических явлениях необратимы. Так, доходы отрасли связи зависят от спроса и потребностей клиентуры в ее услугах, рентабельность – от эффективности использования ресурсов производства, а не наоборот, хотя формальное сравнение вариации этих показателей может показать их согласованную изменчивость.
При исследованиях корреляционных связей важно помнить, что лишь после того, как выяснена сущность явления, установлены причинно-следственная связь и ее форма, а также определено, что первично, а что вторично, имеет смысл количественно оценивать взаимосвязи между явлениями и моделировать закономерности их развития с помощью приемов статистики.
Применение математического аппарата корреляции и регрессии к изучению показателей работы организаций связи обусловливает необходимость последовательного решения трех задач:
1. обоснование теоретической формы связи;
2. определение параметров аналитического уравнения связи;
3. количественное измерение тесноты связи между результативным и факторными признаками.
Первые две задачи решаются с помощью регрессионного анализа, третья – на основе корреляционного и дисперсионного анализа. Корреляционно-регрессионный анализ, как общее понятие, включает в себя измерение тесноты связи, направление связи и установление аналитического выражения формы связи (уравнения регрессии). Функциональные связи исследуются статистикой связи на основе индексного и балансового методов, корреляционные связи – методов графического изображения, приведения (сравнения) параллельных рядов, аналитических группировок, корреляционно-регрессионного анализа.
Наиболее простым и эффективным способом выявления взаимосвязей между явлениями, с которого начинается корреляционный анализ, является графический метод. Для этого на координатном поле наносят точки, соответствующие значениям изучаемых признаков x и y. На оси абсцисс откладывают значения факторного признака х, на оси ординат – результативного признака y. Совокупность точек образует корреляционное поле. По характеру расположения точек на корреляционном поле можно судить о направлении и силе связи. Если точки беспорядочно разбросаны по полю, то зависимость между переменными отсутствует (рис. 8.1, а); если точки образуют эллипс, т.е. концентрируются вокруг оси, идущей из нижнего левого угла в верхний правый (или наоборот), то имеется прямая (или обратная) зависимость между исследуемыми признаками (рис. 8.1, б, в).
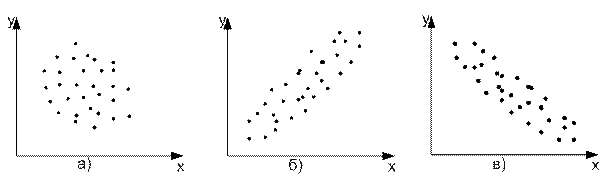
Рис. 8.1. Корреляционное поле при отсутствии зависимости между признаками (а), при наличии прямой зависимости (б), при наличии обратной зависимости (в).
Сущность метода приведения параллельных рядов состоит в сопоставлении рядов, ранжированных по факторным признакам. Для этого все единицы исследуемой совокупности располагают в возрастающем или убывающем порядке по уровню факторного признака, параллельно располагают значения результативного признака. Посредством сопоставления расположенных таким образом рядов выявляется наличие связи и ее направление.
К важнейшим приемам выявления зависимостей между признаками относится метод аналитических группировок.
Для оценки тесноты связи между двумя признаками исчисляется эмпирическое корреляционное отношение h, равное корню квадратному из частного межгрупповой дисперсии к общей дисперсии: 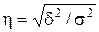 . Коэффициент детерминации h2=d2/s2 показывает, какая часть общей вариации результативного признака объясняется вариацией факторного (группировочного) признака.
. Коэффициент детерминации h2=d2/s2 показывает, какая часть общей вариации результативного признака объясняется вариацией факторного (группировочного) признака.
Следует учитывать, что при группировке значения коэффициента детерминации и корреляционного отношения зависят от числа групп и величины интервалов. Искусство группировки состоит в том, чтобы было образовано такое количество групп, при котором в вариации групповых средних отчетливо проявилось бы влияние группировочного признака. Метод группировки предполагает сравнение не индивидуальных значений факторного и результативного признаков, а групповых средних, которые, являясь обобщающими показателями, выражают корреляционную связь более рельефно, чем при параллельном сравнении рядов.
С широким применением информационных технологий и стандартного программного обеспечения экономических расчетов в отрасли связи все большее распространение получает корреляционно-регрессионный метод анализа взаимосвязей, позволяющий строить модели сложных явлений, выявлять факторы изменения экономических показателей в зависимости от различных причин и рассчитывать вероятные значения исследуемых показателей при определенных условиях и в будущем.
Обычно исследование экономических явлений начинается с изучения парных связей между результативным признаком и каждым из определяющих его факторов. Однако изучение только парных зависимостей оказывается малоэффективным при использовании полученных результатов в планировании, так как действительности свойственна множественность взаимосвязей и исследовать социально-экономические явления необходимо комплексно.
Уровень какого-либо результативного показателя зависит от множества взаимосвязанных факторов, действующих с разной силой и в противоположных направлениях; их влияние на результативный показатель нельзя рассматривать как простую сумму изолированных парных влияний. Это обусловливает ограниченность использования парных уравнений регрессии и построения однофакторных моделей. В условиях действия множества факторов показатели парной связи оказываются условными и неточными. Специфика корреляционных связей требует построения многофакторных моделей – уравнений множественной регрессии.
 2014-01-25
2014-01-25 1258
1258
