Евклидово векторное пространство

Базис и координаты в векторном пространстве.

Определение. Пусть в векторном пространстве L выполнены еще две аксиомы:

А9. Существуют n линейно независимых векторов;

А10. Любые n +1 векторов линейно зависимы.

Тогда говорим, что векторное пространство L имеет размерность n и пишем dim L = n. Для векторного пространства размерности n используется обозначение Lⁿ.

Определение. Базисом в Lⁿ называется любая система, состоящая из n линейно независимых векторов. Векторы, входящие в базис, называются базисными.

Пусть B ={ e ₁, e ₂,…, e _n } – базис в Lⁿ, а x Î Lⁿ – любой вектор. Тогда система { x, e ₁, e ₂,…, e _n } состоит из n +1 векторов, а значит, эти векторы линейно зависимы. Пусть

l_o x +l₁ e ₁+l₂ e ₂+…+l _n e _n = o, (*)

и комбинация нетривиальная. Тогда обязательно l_o¹0. Действительно, предположим противное: l_o= 0. Тогда среди l₁,l₂,…,l _n есть хотя бы одно ненулевое число, и мы получаем условие линейной зависимости базисных векторов:

l₁ e ₁+l₂ e ₂+…+l _n e _n = o.

Но эти векторы по определению линейно независимы. Противоречие.

Поэтому l_o¹0. Тогда из (*) получаем

x = e ₁+ e ₂+…+ e _n.

Обозначим x_i = –l _i /l_o, i =1,…, n, и получим что

x = x ₁ e ₁+ x ₂ e ₂+…+ x_n e _n. (2)

Определение. Выражение (2) называется разложением вектора x по базису B. Числа x ₁, x ₂,…, x_n называются координатами вектора x в базисе B. Пишем: x (x ₁, x ₂,… x_n) _B.

Если y = y ₁ e ₁+ y ₂ e ₂+…+ y_n e _n, то

x + y = (x ₁+ y ₁) e ₁+(x ₂ + y ₂) e ₂+…+( x_n + y_n) e _n,

l x = l x ₁ e ₁+l x ₂ e ₂+…+l x_n e _n.

Таким образом, при сложении векторов их координаты складываются, а при умножении вектора на число его координаты умножаются на это число.

Сопоставим каждому вектору x (x ₁, x ₂,… x_n) столбец, составленный из его координат:

x (x ₁, x ₂,… x_n) «X =, y (y ₁, y ₂,… y_n) «Y =,

x + y «X + Y = ,l x «l X =,

Мы видим, что операциям над векторами соответствуют точно такие же операции над их координатными столбцами. Поэтому с точки зрения линейной алгебры произвольное векторное пространство Lⁿ устроено точно также, как и R ⁿ. Говорят, что Lⁿ изоморфно R ⁿ или, что R ⁿ является моделью пространства Lⁿ.

Замечание. Более точное определение изоморфизма векторных и евклидовых пространств изучается в курсе алгебры. Рекомендуется также ознакомиться с темой, как изменяются координаты вектора при замене базиса.

Определение. Пусть в векторном пространстве L задана ещё одна операция, сопоставляющая двум векторам x и y число x · y, так, что выполнены следующие аксиомы. " x, y, z Î L и "lÎ R

А11. x · y = x · y;

А12. x ·(y + z)= x · y + x · z;

А13. (l x)· y = l(x · y);

А14. x · x ³0 и x · x =0 Û x = o.

Тогда данная операция называется скалярным произведением векторов, а пространство L вместе с этой операцией называется евклидовым пространством. Число x ²= x · x называется скалярным квадратом вектора x.

Обозначение Eⁿ означает евклидово пространство размерности n.

Если вместо А14 выполнено

А14¢. " x Î L $ y Î L такой что x · y ¹0,

то пространство L вместе с такой операцией называется псевдоевклидовым пространством.

Определение. Длиной вектора x в евклидовом пространстве называется число | x |=. Углом между векторами x и y называется такое число a, что cosa=. Векторы x и y называются коллинеарными, если $lÎ R такое, что y =l x.

£1 Û | x · y |£| x | · | y | Û (x · y)²£| x |² · | y |²Û

Û (x · y)²£(x · x)(y · y) (3)

Это неравенство называется неравенством Коши-Буняковского. Докажем его.

1 случай. Векторы x и y не коллинеарны. Тогда "lÎ R y ¹l x, т.е.l x + y ¹ o. Тогда согласно А14 "lÎ R

(l x + y) · (l x + y) >0 Û l²(x·x)+2l(x·y) + y·y >0

Выражение в левой части неравенства представляет собой квадратный трехчлен относительно переменной l. Поскольку это выражение строго больше нуля, то для его дискриминанта получаем

=(x·x)(y · y)– (x · y)²<0.

Значит, имеет место (1) со строгим неравенством.

2 случай. x || y. Тогда $lÎ R такое, что y =l x. Подставим это равенство в (3):

(x ·l x)²£(x · x)(l x ·l x) Û l²(x·x)²£l²(x·x)².

Таким образом, имеет место (3) со знаком равенства.

Попутно мы выяснили, что равенство в (3) достигается тогда и только тогда, когда x || y.

Для векторов в геометрическом пространстве имеет место неравенство треугольника

| x + y |£| x | + | y | (4)

Докажем его для произвольного евклидова пространства. Используя неравенство (1) в виде (x · y)²£| x |²| y |² получаем

| x + y |²=(x + y)·(x + y)= x ²+2 x·y + y ²£| x |²+2| x |² · | y |² + | y |²=(| x | + | y |)².

Остается извлечь корень из обеих частей неравенства. При этом, равенство в (2) имеет место тогда и только тогда, когда равенство имеет место в (1), т.е. когда x || y.

Определение. Векторы x и y называются ортогональными, если x · y =0.

Заметим, что только нулевой вектор ортогонален каждому вектору. Действительно, если " y Î Eⁿ x · y =0, то это должно быть выполнено и для y = x, т.е. x · x =0. В силу А14 это равносильно x = o.

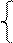Определение. Система векторов { e ₁, e ₂,…, e _k }Î Eⁿ называется ортонормированной, если все векторы единичные и взаимно ортогональные, т.е. " i, j =1… k выполнено e _i · e _j =d _ij = (напомним, что d _ij называется символом Кронекера).

Предложение. Ортонормированная система векторов линейно независима.

Действительно, пусть

l₁ e ₁+l₂ e ₂+…+l _k e _k = o.

Выберем произвольное i =1… k и домножим обе части равенства скалярно на e ₁:

(l₁ e ₁+l₂ e ₂+…+l _k e _k) ·e ₁ = o·e _i Û l₁ e ₁ ·e ₁+l₂ e ₂ ·e ₁ +…+l _k e _k ·e ₁ = 0

Отсюда

l₁ · 1 +l₂ · 0 +…+l _k · 0 = 0 Û l₁ =0.

Аналогично, домножая на l₂получим l₂=0 и т.д. Итак, l₁= l₂=…=l _k = 0.

В курсе алгебры доказывается следующая теорема.

Теорема. В Eⁿсуществует ортонормированный базис (ОНБ), т.е. ортонормированная система, состоящая из n векторов (без доказательства).

Пусть B ={ e ₁, e ₂,…, e _n } – ОНБ в Eⁿ, x, y Î Eⁿ – произвольные векторы. Пусть x (x ₁, x ₂,… x_n) _B, y (y ₁, y ₂,… y_n) _B. Тогда

x · y =(x_i e _i) · (y_j e _j) = x_iy_j (e _i ·e _j) = x_iy_j d _i_j = x_iy_i.

Итак,

x · y = x ₁ y ₁+ x ₂ y ₂+…+ x_n y_n, (5)

т.е. в ОНБ формула для вычисления скалярного произведения такая же, как и в обычном геометрическом пространстве, если координаты заданы в декартовой СК.

Из этой формулы следует, что

| x |=. (6)

Примеры. 1. Пространство V ³ с обычным скалярным произведением векторов: · =||½½ cosÐ(,) представляет собой евклидово пространство. Аксиомы А11 – А14 в точности совпадают со свойствами этого произведения. Базис B ={ i, j, k } представляет собой ОНБ.

2. В пространстве R ⁿ для столбцов

X =, Y =.

определим

X · Y = x ₁ y ₁+ x ₂ y ₂+…+ x_n y_n. (7)

Упражнение 1. Проверьте самостоятельно, что при таком определении выполняются А11 – А14.

Таким образом, R ⁿ со скалярным произведением (7) представляет собой евклидово векторное пространство. Легко проверить, что столбцы

E ₁ =, E ₂=,..., E_n =

составляют ОНБ.

Мы уже отмечали, что для любого векторного пространства Lⁿ векторное пространство R ⁿ может служить его моделью. Для этого надо в Lⁿ выбрать базис B и каждому вектору x (x ₁, x ₂,… x_n) _B сопоставить столбец X, составленный из его координат. Тогда линейным операциям над векторами будут соответствовать точно такие же операции над их координатными столбцами. Выберем теперь в евклидовом векторном пространстве Eⁿ ОНБ B ={ e ₁, e ₂,…, e _n } и по тому же принципу сопоставим каждому вектору его координатный столбец:

x (x ₁, x ₂,… x_n) _B «X =, y (y ₁, y ₂,… y_n) _B «Y =.

Тогда x · y = x ₁ y ₁+ x ₂ y ₂+…+ x_n y_n = X · Y. Таким образом, это соответствие сохраняет не только линейные операции над векторами, но и их скалярное произведение. Поэтому говорят, что Eⁿ изоморфно евклидову векторному пространству R ⁿ или, что евклидово векторное пространство R ⁿ является моделью пространства Eⁿ.

Пусть теперь базис B ={ f ₁, f ₂,…, f _n } в Eⁿ не является ортонормированным. Как вычислить скалярное произведение векторов x (x ₁, x ₂,… x_n) _B, y (y ₁, y ₂,… y_n) _B?