Пример 11.
По группе предприятий, выставивших акции на чековые аукционы в 1996 г., определить с помощью коэффициентов Спирмена зависимость между величиной уставного капитала и количеством выставленных акций.
Таблица 15
| № пред- приятия | Уставной капитал, млн. руб. (X) | Число выставленных акций, (Y) | Ранги | Разность рангов d i = R x - R y | d i2 | |
| R x | R y | |||||
| -8 | ||||||
| -5 | ||||||
| Итого |
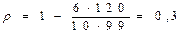 связь слабая.
связь слабая.
Ранговый коэффициент корреляции Кендалла также может использоваться для измерения взаимосвязи между качественными и количественными признаками, характеризующими однородные объекты и ранжированные по одному принципу. Расчет рангового коэффициента Кендалла осуществляется по формуле:
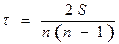
где 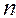 - число наблюдений;
- число наблюдений;
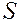 - сумма разностей между числом последовательностей и числом инверсий по второму признаку.
- сумма разностей между числом последовательностей и числом инверсий по второму признаку.
Расчет данного коэффициента выполняется в следующей последовательности:
1. Значения Х ранжируются в порядке возрастания или убывания;
2. Значения У располагаются в порядке, соответствующем значениям X.
3. Для каждого ранга У определяется число следующих за ним значений рангов, превышающих его величину. Суммируя таким образом числа = определяется величина P, как мера соответствия последовательностей рангов по Х и У и учитывается со знаком (+);
4. Для каждого ранга У определяется число следующих за ним значений рангов, меньших его величины. Суммарная величина обозначается через Q и фиксируется со знаком (-);
5. Определяется сумма баллов по всем членам ряда. В приведенном dsit примере
Р= 1 + 8 + 1 + 6 + 4 + 3 + 3 + 2 +1 = 29
Q = (-8) + 0 + (-6) + 0 + (-1) + (-1) + 0 + 0 + 0 = -16
Таким образом:
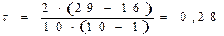
что свидетельствует о практическом отсутствии связи между рассматриваемыми признаками.
Как правило, коэффициент Кендалла меньше коэффициента Спирмена. При достаточно большом объеме совокупности значения данных коэффициентов имеют следующую зависимость:
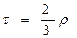
Связь между признаками признается статистически значимой, если значения коэффициентов ранговой корреляции Спирмена и Кендалла больше 0,5.
Для определения тесноты связи между произвольным числом ранжированных признаков применяется множественный коэффициент ранговой корреляции (коэффициент конкордации) W, который вычисляется по формуле:
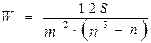 ,
,
где т - количество факторов, n - число наблюдений, S - отклонение суммы квадратов рангов от средней квадратов рангов.
Ранговые коэффициенты Спирмена, Кендалла и конкордации имеют то преимущество, что с помощью их можно измерять и оценивать связи как между количественными, так и между атрибутивными признаками, которые поддаются ранжированию.
 2014-01-25
2014-01-25 761
761








