2014-01-25
733
Признак перпендикулярности плоскостей:
Плоскость перпендикулярна другой, если она проходит через перпендикуляр к этой плоскости.
Плоскость перпендикулярна другой плоскости, если она перпендикулярна прямой, лежащей в этой плоскости.
Итак, зная, как располагаются проекции прямой, перпендикулярной плоскости, легко строить взаимно-перпендикулярные плоскости. Исходя из признака перпендикулярности плоскостей можно:
1) построить перпендикуляр к заданной плоскости и через него провести искомую плоскость
или
2) в заданной плоскости взять прямую и перпендикулярно ей провести искомую плоскость.
В любом из этих случаев задача будет иметь бесчисленное множество решений, если на искомую плоскость не наложены дополнительные условия.
Рассмотрим два примера построения перпендикулярных плоскостей.
Пример: Через точку А провести плоскость, перпендикулярную плоскости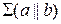 
.
Вариант 1:
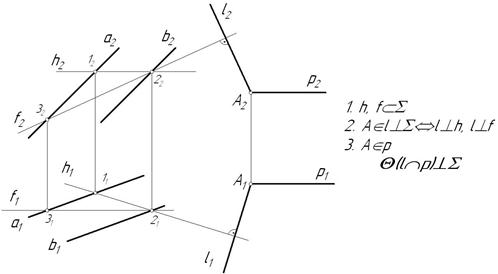
Рис. 4.10
Новая плоскость задана двумя пересекающимися прямыми, одна из которых отвечает условию перпендикулярности плоскостей (прямая l), в зависимости от выбора второй прямой, искомая плоскость может занимать различное положение в пространстве. В данном случае прямая p – профильно-проецирующая, следовательно, сама плоскость является профильно-проецирующей плоскостью.
Вариант 2:
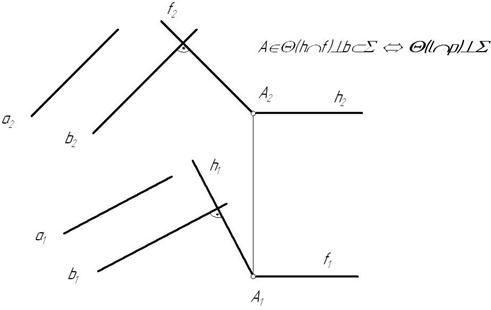
Рис. 4.11
