2014-01-25
707
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО- ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
Контрольные вопросы
1. Дайте определение уравнения линии на плоскости.
2. Приведите формулы различных видов уравнения прямой на плоскости (в пространстве).
3. Приведите формулу вычисления угла между прямыми на плоскости (в пространстве).
4. Сформулируйте условия параллельности и перпендикулярности двух прямых на плоскости (в пространстве).
5. Как найти расстояние от точки до прямой на плоскости (в пространстве)?
6. Докажите, что если две прямые параллельны, то их уравнения можно представить в таком виде, что они будут отличаться только свободными членами.
7. В чем заключается метод координат на плоскости?
8. Как расположены точки, имеющие одну и ту же проекцию на ось Ох? на ось Оу?
9. Как расположена точка в прямоугольной системе координат, если одна ее координата равна нулю? две ее координаты равны нулю?
10. Докажите, что во всяком прямоугольном треугольнике длина медианы, соединяющей вершину прямого угла с серединой гипотенузы, равна половине гипотенузы.
11. Приведите формулы уравнений плоскости в пространстве.
12. Приведите формулу угла между плоскостями.
13. Приведите формулу угла между прямой и плоскостью.
14. Какие линии называются кривыми второго порядка?
15. Дайте определение окружности, приведите ее геометрические свойства.
16. Найдите уравнение касательной к окружности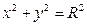 
в точке 
.
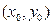17. Дайте определение эллипса, приведите его геометрические свойства.
18. Выведите условие, при котором прямая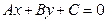 
касается эллипса 
.
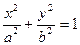19. Докажите, что отношение расстояний от любой точки эллипса до фокуса и соответствующей директрисы есть величина постоянная, равная ɛ.
20. Дайте определение гиперболы, приведите ее геометрические свойства.
21. Докажите, что длина перпендикуляра, опущенного из фокуса на одну из асимптот гиперболы, равна мнимой полуоси.
22. Выведите условие, при котором прямая 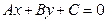касается гиперболы 
.
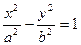23. Дайте определение параболы, приведите ее геометрические свойства.
24. Сформулируйте алгоритм приведения уравнений кривых второго порядка к каноническому виду.
КАФЕДРА ЭКОНОМИКО-МАТЕМАТИЧЕСКИХ МЕТОДОВ И МОДЕЛЕЙ
