Решение. Уравнение плоскости Р1 найдем по формуле (2)

Уравнение плоскости Р₁ найдем по формуле (2):

, ,

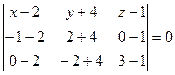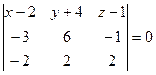т.е. 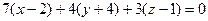или .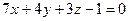

По уравнениям плоскостей определим их нормальные векторы: 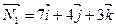, 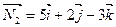. Угол φ между плоскостями Р₁ и Р₂ найдем по формуле (6):

,

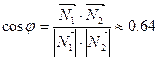откуда .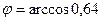

7. Пусть заданы две плоскости Р₁ и Р₂ в виде общих уравнений плоскостей 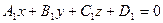, 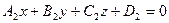соответственно.

Условие параллельности плоскостей. Для того чтобы плоскости Р₁ и Р₂ были параллельны, необходимо и достаточно, чтобы .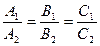

8. Условие перпендикулярности плоскостей. Для того чтобы плоскости Р₁ и Р₂ были перпендикулярны, необходимо и достаточно, чтобы .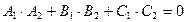

9. Расстояние от точки до прямой. Если прямая 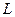задана уравнением 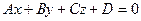и точка 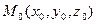не принадлежит данной прямой, то расстояние от точки до прямой находится по формуле

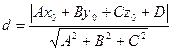. (7)

Лекция 5