2014-01-25
730
1. Преобразуем данное уравнение, использовав формулы поворота осей координат:
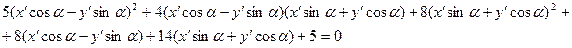
или
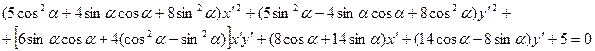
Найдем α из условия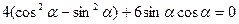 
, т.е. приравняем к нулю коэффициент при 
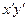. Получим уравнение 
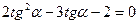. Отсюда 
, 
.
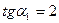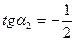Заметим, что эти значения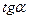 
соответствуют двум взаимно перпендикулярным направлениям. Поэтому, взяв 
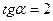вместо 
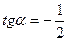, мы только меняем ролями ос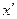и 
и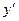 
(рис. 9).
 |
Рис. 9
Пусть 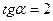, тогда 
, 
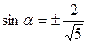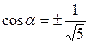; возьмем положительные значения sinα и cosα. Тогда уравнение принимает вид
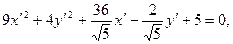или
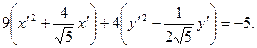
2. Выражения, стоящие в скобках, дополним до полных квадратов:
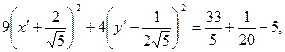
или
.
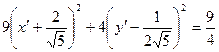Приняв за новое начало точку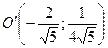 
, применим формулы преобразования координат 
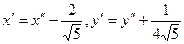, получим
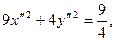или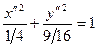 
(уравнение эллипса).
