Если х принадлежит интервалу (a;b)
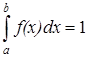
Вывод: Рассмотренные свойства-
1. Вся кривая распределения лежит не ниже оси ox.
2. Площадь криволинейной трапеции, ограниченная кривой распределения и осью ox равна 1.
Пример:
Случайная величина задана функцией
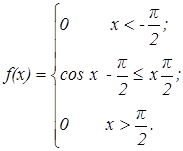
Найти вероятность попадания величины на участок от 0 до p/4. Найти значение коэффициента a и построить кривую распределения.
P (0<x<p/4)=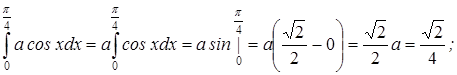
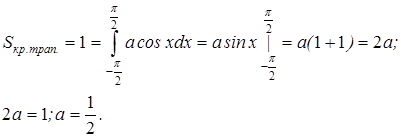
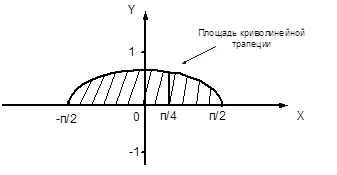 |
Нахождение функции распределения по известной функции f(x).
Установим выражение функции распределения через плотность распределения.
По определению f(x) – это есть вероятность того, что F(x)=P(X)<x. Чтобы применить формулу запишем
F(x)=P(X<x)=P(-¥<X<x),
а по формуле P(a<x<b)=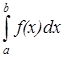 , тогда мы можем записать, что
, тогда мы можем записать, что
F(x)=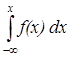
Пример.
Плотность распределения x задана формулой:
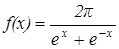
Найти F(x)-?
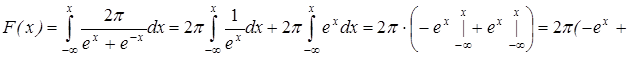
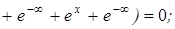
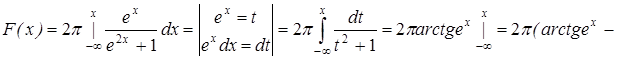
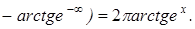
 2014-01-25
2014-01-25 740
740








