Среднее квадратическое отклонение. Роль математического ожидания и дисперсии на практике

Роль математического ожидания и дисперсии на практике

Пример 1: Если нужно сравнить две марки стали по уровню ударной вязкости, что достаточно для каждой марки стали вычислить математическое ожидание ударной вязкости. Лучшей будет та марка стали, у которой математическое ожидание окажется выше

Пример 2: При одинаковом значении математического ожидания более качественным является стальной лист, имеющий минимальный разброс механических свойств. Тот лист лучше, у которого меньше значение дисперсии, т.е. меньше разброс механических свойств.

Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относятся среднее квадратическое отклонение, определяемое по формуле:

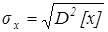Дисперсия квадрата совпадает с размерностью х - средним квадратическим отклонением.