Распределение Пуасcона

Случайная величина x, которая принимает значение m, с вероятностью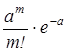, где m =0,1… m называется распределенной по закону Пуассона.

Найти М[x] и D[x].

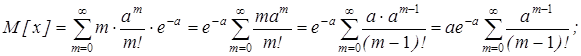
ПРОПУСКАЮ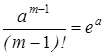--это формула Тейлора.

Таким образом, M[x]=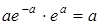; a=n×p, где a - математическое ожидание.

D[x]=a.

Это свойство применяется на практике для решения вопросов правдоподобна ли гипотеза о том, что величина x распределена по закону Пуассона. Для этого определяют оценки математического ожидания, дисперсии, если их значения близки, это может служить доводом в пользу гипотезы о Пуассоновском распределении. Резкое различие этих характеристик напротив свидетельствует против гипотезы.

3. Показательное распределение.

Если случайная величина x имеет показатель распределения, если плотность распределения вероятность ее задана формулой.

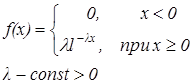
Найдем математическое ожидание, величина непрерывная, то

;

.

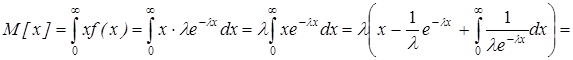
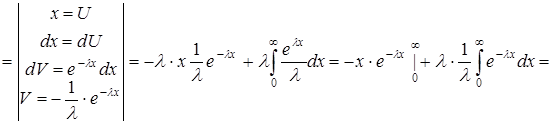
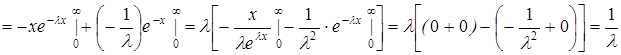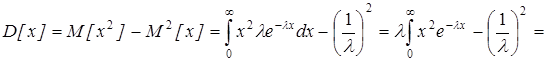
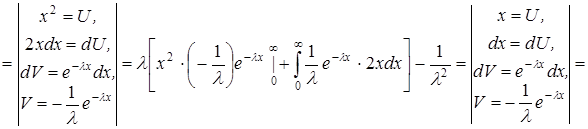
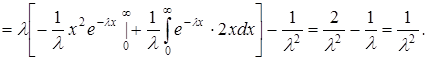
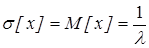На практике: по данным наблюдений находят оценки математического ожидания и дисперсии. Если оценки математического ожидания и дисперсии окажутся близкими одна к другой, то заключают, что изучаемая величина распределена по показательному закону.

4. Равномерное распределение

Если плотность распределения задана формулой

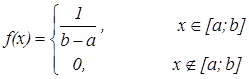
Найдем математическое ожидание

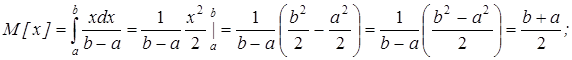
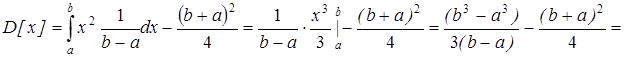
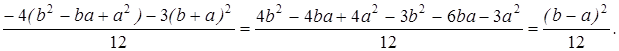
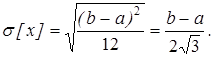
5. Нормальное распределение или закон Гаусса

Задается плотностью распределения вероятности

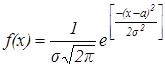
Числовые характеристики для нормированного стандартного распределения, когда s =1, а =0.

,

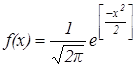График представляет собой четную функцию

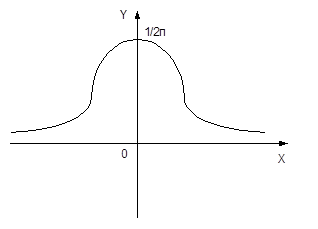Математическое ожидание равно нулю.

М[х]= 0

;

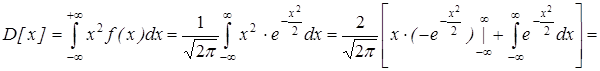
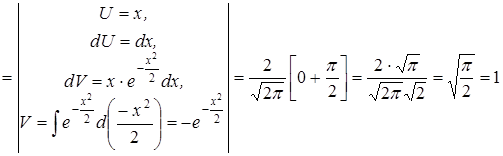D[x]= 1; a=M[x];

; ;

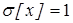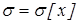Пусть случайная величина у имеет общее и нормальное распределение,

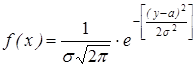
тогда ее (у) можно рассматривать как линейную функцию от случайной величины x, с нормированным распределением.

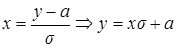
Найдем М[у]

M[y]=M[sx]+M[a]=a

Также D [y]=D[s_x]+D[a]=s²D[х]+0=s² – это есть дисперсия

а – центр распределения

s² – дисперсия распределения