Моделирование сезонных колебаний

Простейший подход к моделированию сезонных колебаний – это расчет значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда.

Общий вид аддитивной модели следующий:

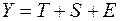. (4.3)

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (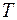), сезонной (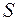) и случайной (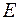) компонент.

Общий вид мультипликативной модели выглядит так:

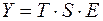. (4.4)

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (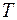), сезонной (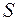) и случайной (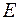) компонент.

Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.

Построение аддитивной и мультипликативной моделей сводится к расчету значени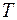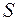й , и 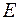для каждого уровня ряда.

Процесс построения модели включает в себя следующие шаги:

1) Выравнивание исходного ряда методом скользящей средней.

2) Расчет значений сезонной компоненты .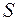

3) Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных (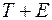) в аддитивной или (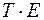) в мультипликативной модели.

4) Аналитическое выравнивание уровней (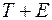) или (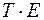) и расчет значений 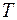с использованием полученного уравнения тренда.

5) Расчет полученных по модели значений (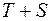) или ().

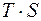6) Расчет абсолютных и/или относительных ошибок. Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок 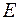для анализа взаимосвязи исходного ряда и других временных рядов.