2014-01-25
835
При вычислении коэффициентов Фурье на отрезке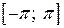 
, симметричном относительно нуля, следует пользоваться свойствами определенного интеграла от четной или нечетной функции. Если функция 
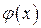– четная, а 
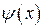– нечетная, то
; 
.
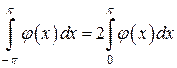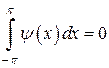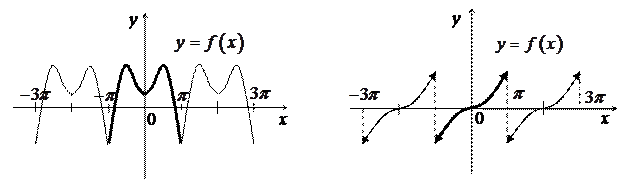
В случае четной периодической функции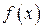 
(рис. 3а) имеем: 
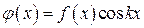– четная функция, 
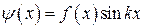– нечетная функция, поэтому формулы для вычисления коэффициентов Фурье преобразуются к виду:
; 
, 
; 
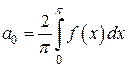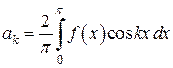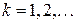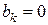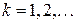, (13)
Таким образом, четная функция 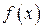раскладывается в ряд Фурье только по косинусам, а коэффициент 
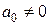«регулирует» сдвиг графика функции по оси ординат.
В случае нечетной периодической функции 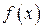(рис. 3б) имеем: 
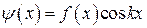– нечетная функция, 
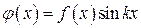– четная функция. Применив формулы (32) и (33), получаем:
; 
, ; 
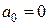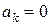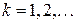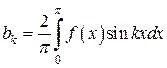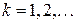, . (14)
Нечетная функция 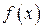раскладывается в ряд Фурье только по синусам, а сдвиг графика функции по оси ординат отсутствует 
.
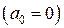6.6. Разложение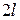 
-периодических функций в ряд Фурье
Теорию тригонометрических рядов Фурье для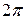 
-периодических функций с помощью линейного отображения (замены переменной):
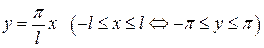(15)
можно перенести на случай произвольных 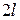-периодических функций. При этом 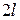-периодической функции 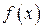соответствует ряд Фурье вида:
|
|
|
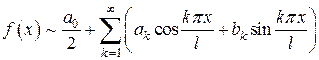, (16)
В силу однозначного соответствия (15) все изложенные выше факты теории рядов Фурье вида (4) можно перенести на ряды вида (16).
Общие формулы коэффициентов тригонометрического такого ряда, имеют вид:
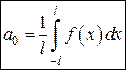; (17) 
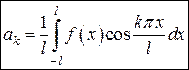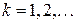, ; (18)
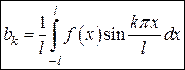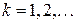, . (19)
Для четной 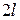-периодической функции 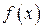выполняется:
; 
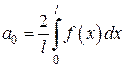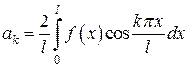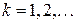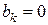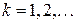, ; , (20)
а для нечетной 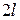-периодической функции 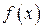справедливо:
; , ; 
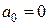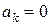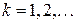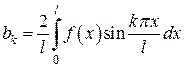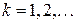, (21)
