Ряды Фурье
Метод Гаусса – Жордана.



2. Метод простых итераций










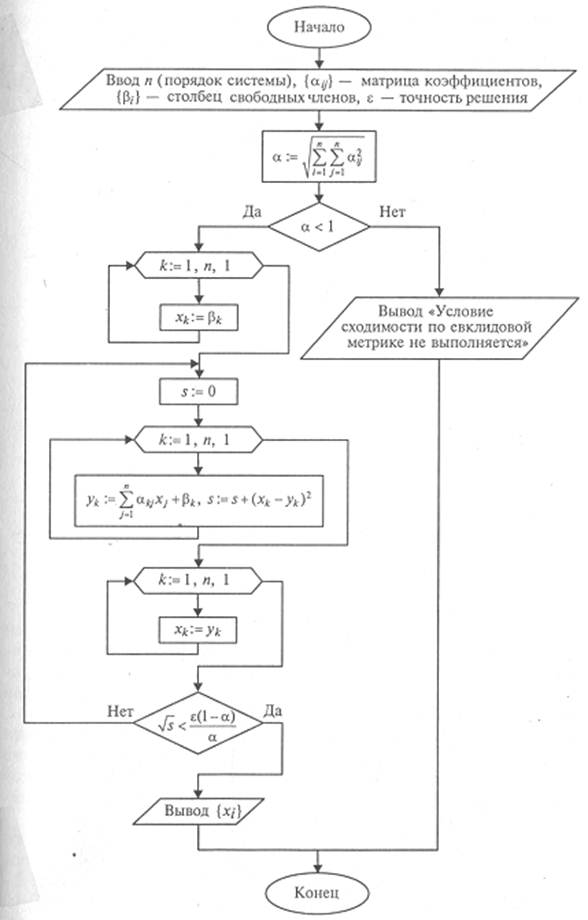 3. Метод Зейделя.
3. Метод Зейделя.




3) методом Гаусса – Зейделя.

Если 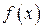 является функцией периодической, то естественно раскладывать ее в функциональный ряд также по периодическим функциям, например, по косинусам и синусам.
является функцией периодической, то естественно раскладывать ее в функциональный ряд также по периодическим функциям, например, по косинусам и синусам.
Тригонометрическим рядом называется функциональный ряд вида:
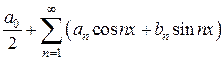 (1)
(1)
числа 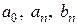
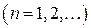 называются коэффициентами тригонометрического ряда;
называются коэффициентами тригонометрического ряда;
или, в более общем виде, ряд:
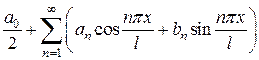 , (2)
, (2)
где 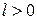 – постоянное число.
– постоянное число.
Тригонометрические ряды широко применяются для изучения различных периодических процессов в электротехнике, радиотехнике, в теории упругих механических колебаний и во многих других областях естествознания и техники. Разложение функций в тригонометрический ряд называется гармоническим анализом, ибо этим достигается разложение какого-либо сложного периодического явления на простые гармонические колебания.
Примерно с середины XVIII в. Д. Бернулли, Ж. Даламбер, Ж. Лагранж и Л. Эйлер, изучавшие некоторые проблемы математической физики, оказались вовлеченными в дискуссию по поводу возможности представления «произвольной» 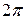 -периодической функции в виде тригонометрического ряда (1). В начале XIX в. работы французского математика Ж. Б. Фурье открыли новую эпоху в развитии теории тригонометрических рядов. Фурье мог представить в виде суммы тригонометрического ряда (в настоящее время называемого рядом Фурье) любую функцию, которую ему в то время могли предложить. Дальнейшее изучение рядов Фурье учеными разных стран способствовало развитию теории интегрирования, теории дифференциальных уравнений, функционального анализа.
-периодической функции в виде тригонометрического ряда (1). В начале XIX в. работы французского математика Ж. Б. Фурье открыли новую эпоху в развитии теории тригонометрических рядов. Фурье мог представить в виде суммы тригонометрического ряда (в настоящее время называемого рядом Фурье) любую функцию, которую ему в то время могли предложить. Дальнейшее изучение рядов Фурье учеными разных стран способствовало развитию теории интегрирования, теории дифференциальных уравнений, функционального анализа.
В XIX в. разложения функций в ряды Фурье использовались в основном для решения задач математической физики и дифференциальных уравнений в частных производных. Применение метода разделения переменных (метода Фурье) для решения уравнения колебания струны подробно описано в учебнике [1] и более сжато – в методических указаниях [5].
Исторически проблема разложения функции в тригонометрический ряд формулировалась очень просто. Пусть дано равенство:
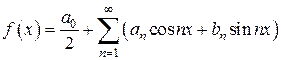 , (3)
, (3)
где 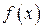 – известная
– известная 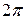 -периодическая функция. Каковы должны быть коэффициенты ряда
-периодическая функция. Каковы должны быть коэффициенты ряда 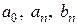 и какие дополнительные условия на функцию требуется наложить, чтобы равенство (3) было справедливо?
и какие дополнительные условия на функцию требуется наложить, чтобы равенство (3) было справедливо?
Формулы коэффициентов тригонометрического ряда, порождаемого данной функцией 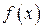 , впервые были получены Фурье. Способ получения был красив и одновременно нестрог, ибо предполагалось, что функциональный ряд можно почленно интегрировать.
, впервые были получены Фурье. Способ получения был красив и одновременно нестрог, ибо предполагалось, что функциональный ряд можно почленно интегрировать.
6.2. Вывод формулы для а 0.
Домножим левую и правую части равенства (3) на 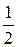 , являющуюся первой функцией ПТС (11). Имеем:
, являющуюся первой функцией ПТС (11). Имеем:
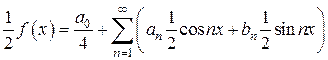 . (4)
. (4)
Проинтегрируем обе части равенства (4) почленно на отрезке 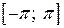 и воспользуемся ортогональностью функций. Получаем цепочку преобразований:
и воспользуемся ортогональностью функций. Получаем цепочку преобразований:
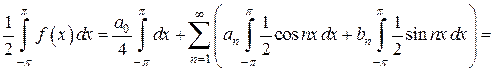
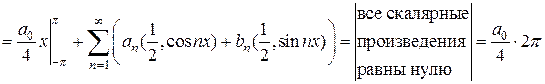 .
.
В итоге имеем уравнение 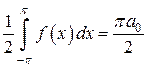 , из которого получаем
, из которого получаем 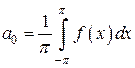 .
.
6.3. Вывод формул для ak, bk.
Домножим левую и правую части равенства (4) на одну из функций вида 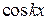 при некотором фиксированном
при некотором фиксированном 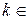 N. Имеем:
N. Имеем:
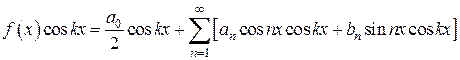 . (5)
. (5)
Проинтегрируем обе части равенства (5) почленно на отрезке 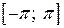 и воспользуемся свойством ортогональности. Получаем:
и воспользуемся свойством ортогональности. Получаем:
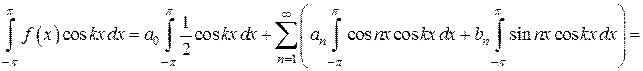
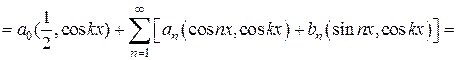
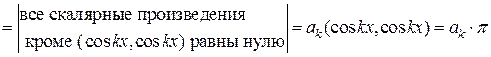 .
.
В итоге имеем уравнение 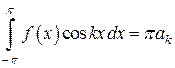 , из которого получаем
, из которого получаем 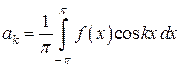 .
.
Аналогичным образом можно установить, что  , откуда
, откуда 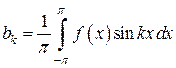 .
.
В итоге наших преобразований получены формулы коэффициентов тригонометрического ряда (1), соответствующего функции 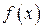 :
:
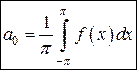 ; (6)
; (6) 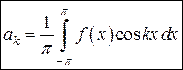 ,
, 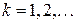 ; (7)
; (7)
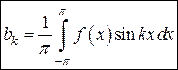 ,
, 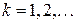 . (8)
. (8)
Опр. Коэффициенты, определяемые формулами (6) – (8) называются коэффициентами Фурье функции 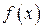 , а тригонометрический ряд (1) с такими коэффициентами – рядом Фурье функции
, а тригонометрический ряд (1) с такими коэффициентами – рядом Фурье функции 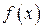 .
.
Для интегрируемой на отрезке 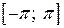 функции
функции 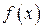 записывают
записывают
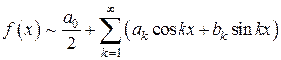 (9)
(9)
и говорят: функции 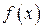 соответствует ее ряд Фурье. Если ряд Фурье сходится, то его сумму обозначим
соответствует ее ряд Фурье. Если ряд Фурье сходится, то его сумму обозначим 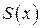 .
.
 2014-01-25
2014-01-25 778
778








