Необходимый признак сходимости ряда

Теорема 1. Если ряд (1.1) сходится, то его общий член стремится к нулю:

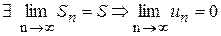(2.1)

Доказательство:

Пусть ряд 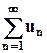сходится. Тогда по определению существует 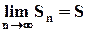- конечное число. Но тогда и 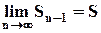, так как, если 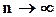, то и 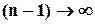. Но так как 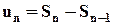, то .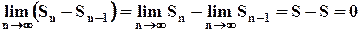

Следствие. Если 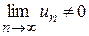, то ряд (1.1) расходится

Замечание: По необходимому признаку сходимости нельзя сделать вывод о сходимости ряда, но если необходимый признак ряда не выполняется (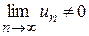), то можно сделать вывод о его расходимости.

Теорема 2. (Свойства сходящихся рядов)

Свойство 1. Если сходятся ряды:

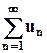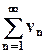(1) (2)

И их суммы равны соответственно 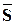и 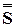, то ряд 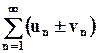также сходится и его сумма равна .

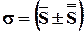Доказательство:

Пусть 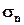– «n»–ная частичная сумма рассматриваемого ряда, тогда 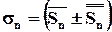. Далее, из определения предела следует, что:

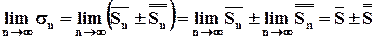
Свойство 2. Если сходится ряд: 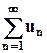и его сумма равна 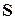, тогда ряд 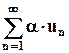, где 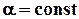также сходится и его сумма равна 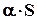. Доказательство аналогично (провести самостоятельно).

Ряд, получающийся из исходного ряда 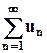путём отбрасывания конечного числа его первых членов называется остатком ряда. Остаток ряда есть в свою очередь также ряд.

Теорема 3. Ряд 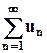сходится тогда и только тогда, когда сходится его остаток.

Доказательство:

Рассмотрим частичную сумму ряда: 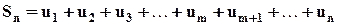(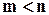) или

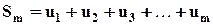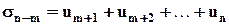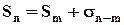, , . Здесь величина 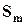– есть постоянное число. Если исходный ряд сходится, то существует конечный предел последовательности частичных сумм: 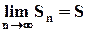, но 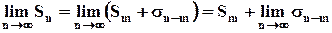и тогда из существования конечного предела в левой части равенства влечёт существование предела в правой части и наоборот.

Т.о. отбрасывание конечного числа членов ряда не влияет на его сходимость.

При изучении рядов, как правило, решаются две задачи: исследование на сходимость или расходимость, нахождение суммы ряда в случае его сходимости. Последний вопрос является существенно проблематичнее и не всегда решаем.