Лекция №3 второе уравнение Максвелла

УРАВНЕНИЯ МАКСВЕЛЛА И ИХ РЕШЕНИЕ

Учебные вопросы:

1. Полная система уравнений Максвелла, граничные условия. Интегральная форма уравнений Максвелла.

2. Решение уравнений Максвелла, волновых уравнений. Теорема запаздывающих электродинамических потенциалов.

3. Уравнения Максвелла в комплексной форме.

ВВЕДЕНИЕ

Изучив основные свойства статических и стационарных полей, являющихся частным случаем проявления переменного ЭМП, рассмотрим само ЭМП в общем виде и его свойства. ЭМП - это вид материи, оказывающий силовое воздействие на заряженные частицы, характеризуемый неразрывно связанными друг с другом и меняющимися во времени электрическим и магнитным полями. Используя знания основных уравнений электрического стационарного поля и магнитного поля постоянного тока, получим полную систему уравнений Максвелла (англичанин, 1831-1879. В 1857 - труд "О фарадеевских силовых линиях").

Уравнения Максвелла – основа описания любых электромагнитных полей во всевозможных устройствах средств РТО, поэтому знание этих уравнений – фундамент для грамотной эксплуатации радиоэлектронных средств

1. ПОЛНАЯ СИСТЕМА УРАВНЕНИЙ МАКСВЕЛЛА, граничные условия. ИНТЕГРАЛЬНАЯ ФОРМА УРАВНЕНИЙ МАКСВЕЛЛА

Рассмотренные нами поля: - ЭЛСТ, создаваемое неподвижными и неизменными во времени зарядами (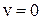, 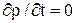); стационарное МП постоянного тока (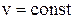), являются частными случаями электромагнитного поля (ЭМП) (рис.1).

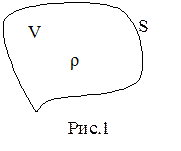Ясно, что уравнения для ЭЛСТ поля 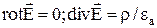и уравнения для стационарного МП 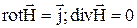должны вытекать из некоторых обобщенных уравнений, справедливых для ЭМП в целом. Следовательно, необходимо получить систему уравнений, описывающих ЭМП заряженных частиц, состояние которых характеризуется скоростью их движения v и величиной заряда, являющегося функцией времени, т.е. .

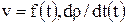Заметим сразу, что полный вывод уравнений Максвелла мы опускаем. Оставим только отправные точки и конечный результат.

Исходя из уравнения непрерывности 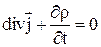, и учитывая, что, например, в диэлектрике помимо тока проводимости присутствует также ток смещения, можно получить первое уравнение Максвелла (I УМ)

,

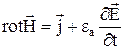устанавливающее связь между переменным во времени электрическим полем и возникающим вокруг него магнитным полем.

Физический смысл: МП возникает не только при движении зарядов, когда имеет место ток проводимости, но и при наличии изменяющегося во времени электрического поля.

Второе уравнение Максвелла (II УМ) вытекает из закона ЭМ индукции Фарадея (1831г.)

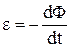
согласно которому, если через поверхность, ограниченную проводящим контуром, проходит меняющийся во времени магнитный поток Ф, то в контуре возникает ЭДС индукции. II УМ имеет вид:

.

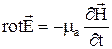Физический смысл: В ЭМП электрическое поле является вихревым. Причиной ЭП, помимо электрических зарядов, является изменяющееся во времени МП.

Итак, полная система дифференциальных уравнений, описывающих ЭМП, включает в себя следующие уравнения:

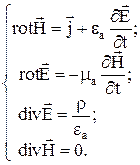
Вспомогательные уравнения: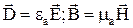

ИНТЕГРАЛЬНАЯ ФОРМА УРАВНЕНИЙ МАКСВЕЛЛА

Интегральным аналогом первого уравнения Максвелла является так называемый закон полного тока или теорема циркуляции (Циркуляция вектора по замкнутому контуру интегрирования равна полному току, протекающему через площадь, охваченную контуром интегрирования).

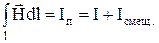
Физический смысл: Токи смещения наравне с токами проводимости образуют магнитное поле. Закон изменения ЭП во времени определяет закон распределения МП в пространстве.

Интегральным аналогом второго уравнения Максвелла является закон электромагнитной индукции

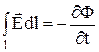
Физический смысл: Переменное магнитное поле образует вихревое электрическое поле. Закон изменения МП во времени определяет закон распределения ЭП в пространстве.

Интегрируя 3-е уравнение Максвелла по объему и применяя формулу Остроградского-Гаусса, получим:

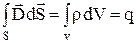
Это равенство называется теоремой Гаусса: поток вектора электрической индукции через произвольную замкнутую поверхность определяется электрическим зарядом q, содержащимся в объеме V, ограниченном поверхностью S.

Подобным образом получим интегральную запись последнего уравнения Максвелла

,

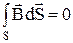выражающую непрерывность линий магнитной индукции. Итак, полная система уравнений Максвелла в интегральной форме имеет вид:

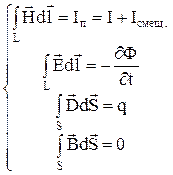
Отметим, что уравнения Максвелла в дифференциальной форме справедливы лишь тогда, когда параметры среды либо не зависят от координат, либо являются непрерывными функциями их. Уравнения Максвелла в интегральной форме применимы во всех случаях, включая и те, когда параметры среды, или хотя бы один из них, изменяются скачками.

2. РЕШЕНИЕ УРАВНЕНИЙ МАКСВЕЛЛА, ВОЛНОВЫХ УРАВНЕНИЙ. ТЕОРЕМА ЗАПАЗДЫВАЮЩИХ ЭЛЕКТРОДИНАМИЧЕСКИХ ПОТЕНЦИАЛОВ

Впервые предположение о том, что ЭМ возмущения носят волновой характер было высказано Фарадеем в 1832 г. Теоретическим подтверждением предположения Фарадея о существовании ЭМВ послужила система уравнений Максвелла.

В настоящее время известно, что если какое-либо явление описывается волновым уравнением Даламбера

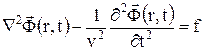, (1)

то его решение

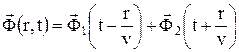(2)

представляет собой пару бегущих волн, распространяющихся соответственно вдоль и против 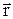с постоянной скоростью v. Физический смысл имеет только первое слагаемое, то есть

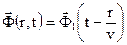(2а)

Это уравнение описывает функцию, изменение которой происходит не моментально, а через время задержки t_з =r/v. Эта функция является запаздывающей. Распространение электромагнитного поля происходит не моментально, а с задержкой. Эти положения теории дальнего действия на основе ограничений Зоммерфельда получили название теоремы запаздывающих электродинамических потенциалов.

Рассмотрим первое уравнение Максвелла в дифференциальной форме. Применив операцию rot к обеим частям этого уравнения, используя формулы векторного анализа и принимая во внимание 2 и 4 уравнения Максвелла, получим

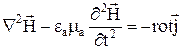. (3)

Аналогично можно показать, что (из II УМ)

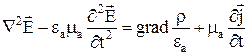. (4)

Для пространства, свободного от зарядов и токов (r=0, j=0), эти уравнения преобразуются к виду

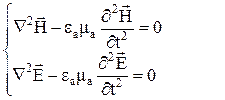(5, 6)

т.е. переходят в однородные волновые уравнения.

Уравнения (3)...(6) имеют вид (2) и носят волновой характер. Сравнивая (3...6) с (1), можно записать, что .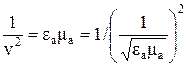

С этого момента мы имеем право говорить об ЭМ волнах, которые распространяются в пространстве со скоростью

.

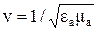Рассмотрим основную задачу электродинамики.

Пусть в некотором объеме задано распределение токов и зарядов, и необходимо определить ЭМП, создаваемое ими. Для этого необходимо решить систему уравнений Максвелла относительно H и E, или, что то же самое, векторные волновые уравнения (3,4) или (5,6). Каждое из этих уравнений распадается на систему из трех скалярных, поэтому общий объем требуемых рассуждений и выкладок оказывается довольно громоздким. Более просто определить H и E с помощью так называемых электродинамических потенциалов j и .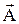

Известно, что для электростатического поля

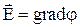, (7)

а для магнитного поля постоянного тока

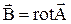. (8)

Очевидно, для ЭМП эти соотношения видоизменяются. Определим их.

Учитывая (8), второе УМ можно записать

,

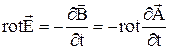или

.

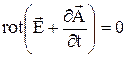Тогда по аналогии с тем, как мы поступили при рассмотрении свойств электростатического поля, и учитывая, что ЭЛСТ поле - частный случай ЭМП, можно записать

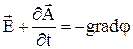, (9)

откуда

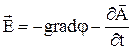
аналогично .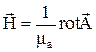

Из этого равенства следует, что электрическая составляющая ЭМП одновременно связана со скалярным j и векторным 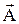потенциалами. Т.е. зная j и 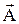, можно определить Е и Н в соответствии с выражениями (8) и (9).

К дальнейшему упрощению приводит введение потенциала Герца на основе уравнений связи .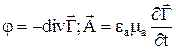

Вектор Герца Г также удовлетворяет векторному волновому уравнению

.

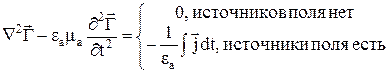Если вектор Герца Г найден, то Е и Н определяются

, ,

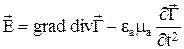
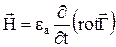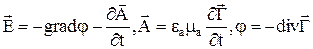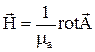
Потенциалы j и А, входящие в решение, удовлетворяют уравнению (2а), поэтому называются запаздывающими потенциалами.

Таким образом, можно решить основную задачу электродинамики, зная скалярный и векторный потенциалы и вводя вспомогательный вектор Герца.

3.УРАВНЕНИЯ МАКСВЕЛЛА В КОМПЛЕКСНОЙ ФОРМЕ

Будем рассматривать гармонические ЭМП, создаваемые гармоническими токами и зарядами. В средствах радиосвязи используются узкополосные радиосигналы, модели которых в радиотехнике принято считать квазигармоническими узкополосными сигналами. Их записывают в гармонической форме.

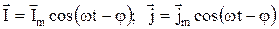
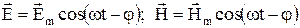
Для анализа таких колебаний удобно воспользоваться символическим методом. Согласно этому методу, гармоническая функция a=A_mcos(wt-j), где a- мгновенное значение функций; A_m – амплитуда; w – угловая частота; j- начальная фаза, может быть заменена комплексной

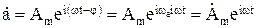
где 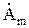– комплексная амплитуда.

Запишем мгновенное значение для векторов в комплексной форме

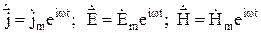
Подставим их в уравнения Максвелла

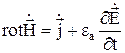
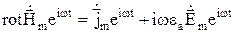
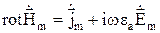– I УМ в комплексных амплитудах.

Аналогично

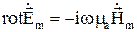– II УМ в комплексных амплитудах.

Однородные волновые уравнения

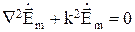
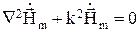
где 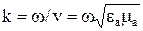- коэффициент распространения (волновое число).

ЗАКЛЮЧЕНИЕ

Таким образом, уравнения Максвелла полностью описывают ЭМП и позволяют решить задачу по определению составляющих поля. Граничные условия позволяют находить компоненты ЭМП в разных граничащих средах, зная параметры среды. Основные теоремы электродинамики позволяют определить расход энергии на распространение радиоволн и возможность проведения экспериментов с моделями, а не с реальными объектами.