Лекция 2. Системы линейных уравнений
2.1. Основные понятия и определения
2.2. Система n линейных уравнений с n переменными. Формулы Крамера
2.3. Теорема Кронекера-Капелли
2.4. Матричный метод. Метод Гаусса
2.5. Общее решение систем линейных алгебраических уравнений
2.6. Системы однородных уравнений
2.1. Oсновные понятия и определения
Определение 1. Система m линейных уравнений с n переменными имеет вид:
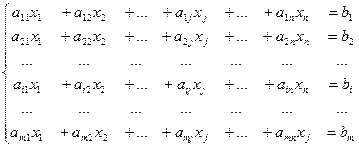
где aij (i =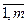 , j =
, j =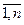 )-коэффициенты при переменных, bi (i =
)-коэффициенты при переменных, bi (i =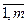 ) - свободные члены.
) - свободные члены.
Краткая запись: 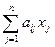 = bi (i =
= bi (i =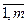 ) (1)
) (1)
Определение 2.Решение системы (1) – совокупность n чисел (x1=k1, x2=k2,...., xn=kn), при подстановке которых каждое уравнение системы обращается в верное равенство.
Определение 3. Система совместна, если она имеет хотя бы одно решение, и несовместна, если решений нет. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Определение 4. Две системы уравнений называются равносильными или эквивалентными, если множества их решений совпадают.
С помощью элементарных преобразований можно от исходной системы переходить к равносильной системе. Если ввести обозначения:
А = 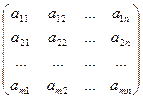 , X=
, X=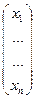 , B=
, B= ,
,
то получаем матричную запись системы (1)
АХ = В (2)
Сформулируем основные задачи, которые возникают при изучении системы (1):
· узнать, является ли система (1) совместной или несовместной;
· если система (1) совместна, то узнать, является ли она определенной;
· если система (1) совместна и определенна, то найти ее единственное решение;
· если система (1) совместна и неопределенна, то описать совокупность всех ее решений.
Эти задачи легко решаются в случае, когда число уравнений системы (1) совпадает с числом неизвестных, т.е. когда m=n.
2.2. Система n линейных уравнений с n переменными.
Формулы Крамера
Если в системе (1) m=n, то хj = 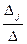 , (j =
, (j =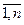 ) (3)
) (3)
где Δ - определитель системы, Δ j (j =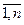 ) определители, полученные из Δ заменой столбца коэффициентов при хj столбцом свободных членов.
) определители, полученные из Δ заменой столбца коэффициентов при хj столбцом свободных членов.
Эти формулы получили название формул Крамера. (Г.Крамер – (1704-1752г.г.) – швейцарский математик).
Если в формулах (3) Δ ≠ 0, то система совместна. Если в формулах (3) Δ = 0, а какое – либо из Δ j≠ 0, то система несовместна.
Если Δ = Δ 1 = …= Δn = 0, то система неопределенная и имеет бесчисленное множество решений.
Пример. Решить систему уравнений по формулам Крамера.
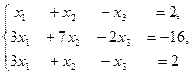
Решение. Δ = 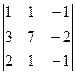 = 10 ≠ 0,
= 10 ≠ 0,
Δ1 = 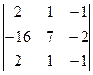 = 0, Δ2 =
= 0, Δ2 = 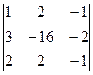 = -40, Δ3 =
= -40, Δ3 = 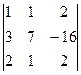 = -60.
= -60.
Отсюда по формулам Крамера получаем: х1 = 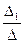 =
= 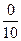 = 0,
= 0,
х2 = 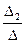 =
= 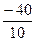 = -4, х3 =
= -4, х3 = 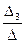 =
= 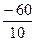 = -6.
= -6.
2.3. Теорема теорема Кронекера – Капелли
(Кронекер Л. (1823 – 1891г.г.), немецкий математик, Капелли (1858-1916г.г.), итальянский математик).
Пусть дана система линейных уравнений 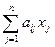 = bi (i =
= bi (i =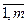 ) (1) Составим расширенную матрицу системы С =
) (1) Составим расширенную матрицу системы С = 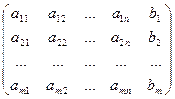 .
.
Теорема Кронекера – Капелли.
Для того, чтобы система (1) была совместной, необходимо и достаточно, чтобы r(A) = r(C). Если r(A) = r(C) = n, то система (1) имеет единственное решение. Если же r(A) = r(C) <n, то система (1) имеет бесчисленное множество решений.
Проиллюстрируем применение этой теоремы рядом примеров.
 2014-01-25
2014-01-25 804
804








