Уравнение энергии

Следуя первому началу термодинамики (закону сохранения энергии), составим баланс энергии в неподвижной системе коор­динат (рис. 2.1), т.е. рассмотрим преобразование энергии в од­ной и той же массе газа, заполнявшей вначале объем 1 — 2, а через бесконечно малый промежуток времени dτ переместив­шейся в положение 1' — 2'.

Приращение любого вида энергии равно разности количеств этого вида энергии в положениях 1’ — 2' и 1 — 2. Ввиду того, что заштрихованный объем 1’ — 2 является общим для этих двух положений, приращение энергии измеряется разностью количеств энергии в бесконечно малых объемах 2 — 2' и. 1 — 1'. Отсюда следует, что приращение кинетической энергии равно

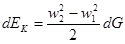(2.5)

здесь dG — массовый расход газа через поперечное сечение струйки за время dτ. Приращение потенциальной энергии (энер­гии положения)

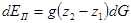(2.6)

где z₂ и z₁ — высоты расположения (нивелирные уровни) сече­ний 2 и 1, g — ускорение силы тяжести. Приращение внутрен­ней (тепловой) энергии

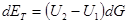(2.7)

где U = c_v-T — тепловая энергия единицы массы газа (произ­ведение теплоемкости при постоянном объеме на абсолютную температуру). Если теплоемкость газа в сечениях 1 и 2 одина­кова, то прирост внутренней энергии равен

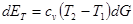(2.8)

На основания выделенной части струйки газа действуют на­правленные внутрь и по нормали к ним внешние силы давле­ния р. При перемещении газа внешние силы давления произво­дят работу. Например, перенос газа из сечения 1 в сечение 1’ происходит как бы под действием поршня площадью F₁ с дав­лением р₁. Работа поршня за время dτ равна

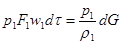(2.9)

Точно так же можно представить себе, что давление р₂ на сече­ние 2 осуществляется поршнем площадью F_2. За время dτ газ переместит поршень в положение 2, производя отрицательную работу

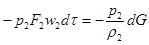
Силы давления, действующие на боковую поверхность струй­ки (поверхность тока), никакой работы не производят, так как они нормальны к траекториям движения частиц газа. Таким об­разом, энергия, внесенная силами давления, равна разности между работами поршня 1 и поршня 2:

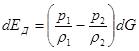(2.10)

К газовой струйке на участке 1 — 2 может быть за время dt подведено тепло в количестве 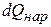. Далее газовая струйка за время dτ может произвести техническую работу dl, например, приводя во вращение колесо турбины, установленное между се­чениями 1 и 2. Наконец, следует учесть энергию, расходуемую газом за время dτ на преодоление сил трения dl_Tp.

Согласно первому началу термодинамики подведенные к газу тепловая энергия и работа сил давления расходуются на со­вершение технической работы, работы сил трения, а также на изменение внутренней энергии

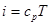(2.11)

Тогда соотношение (2.11) примет несколько иной вид:

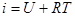(2.12)

или на основании (2.10)

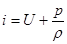(2.13)

Используя выражения (2.6), (2.7) и (2.13), можно придать урав­нению энергии следующую форму:

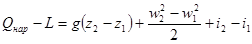(2.14)

Уравнение энергии (2.14) иногда называют также уравнением теплосодержания. Существенно то обстоятельство, что уравнение теплосодержания не содержит работы трения. По­скольку энергия, расходуемая на преодоление трения или любого другого вида сопротивлений, преобразуется полностью в тепло, а последнее остается в газовой струе, наличие сил трения не может нарушить общий баланс энергии, а лишь приводит к преобразованию одного вида энергии в другой.

Обычно в технике приходится иметь дело с частными фор­мами уравнения теплосодержания. Так, в большинстве случаев изменение потенциальной энергии пренебрежимо мало в срав­нении с другими частями уравнения энергии, и членом g(z₂ — z₁) пренебрегают. Тогда уравнение теплосодержания имеет следую­щий вид:

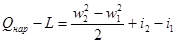(2.15)

При отсутствии технической работы и теплообмена с окру­жающей средой, т. е. в случае энергетически изолированного процесса в газе, имеем

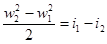(2.16)

В частности, уравнение (2.16) определяет движение газа по трубе, если нет теплопередачи через стенки. Согласно сказанному это уравнение справедливо вне зависимости от того, действуют или нет силы трения. Иначе говоря, изменение теплосодержания (температуры) в энергетически изолированном процессе свя­зано только с изменением скорости. Если скорость газа не ме­няется, то остается постоянной и температура.

Если нет теплообмена, но присутствует техническая работа, то расчет лишь не­много усложнится. Именно:

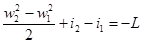(2.17)

Когда технической работы нет, уравнение теплосодержания дает

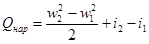(2.18)

в таком виде оно применяется к теплообменным процессам.

Применительно к энергетически изолированным течениям газа, когда выполняются условия

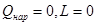(2.19)

и уравнение теплосодержания приобретает форму (2.16). Его можно записать следующим образом

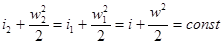(2.20)

Отсюда нетрудно видеть, что если газовую струю затормозить полностью, то теплосодержание газа достигает максимального возможного значения:

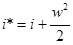(2.21)

Получающееся при этом значение теплосодержания i* называется полным теплосодержанием, а соответствующую абсо­лютная температура

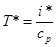(2.22)

— температурой торможения.

Итак, температура газа получается равной температуре тор­можения в том случае, когда скорость течения уменьшается до нуля при отсутствии энергетического обмена с окружающей сре­дой. Пользуясь средним значением теплоемкости, можно вычис­лить температуру торможения по следующей формуле:

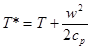(2.23)

Следует подчеркнуть, что, согласно уравнению энергии (2.20), в энергетически изолированном потоке идеального газа сущест­вует однозначная зависимость между температурой газа Т (теп­лосодержанием i) и скоростью течения w. Повышение скорости в таком потоке всегда сопровождается снижением температуры независимо от изменения других параметров газа.