Уравнения вида

Метод решения.

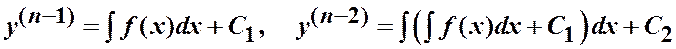
и т. д.

Пример. Решить задачу Коши:

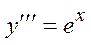, y (1)=0, y ¢(1)=1, y ¢¢(1)=2.

Решение. Интегрируем трижды:

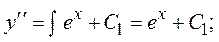
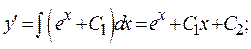
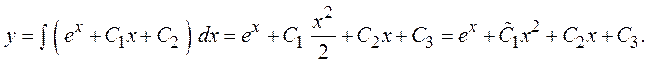
Найдем решение, удовлетворяющее заданным начальным условиям.

y (1) = 0 Þ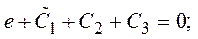

y ¢(1) =1 Þ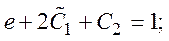

y ¢¢(1) =2 Þ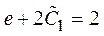

Þ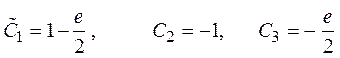

Þ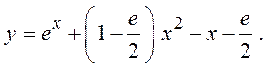

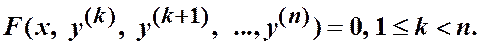
(не содержат искомую функцию и (возможно) несколько ее младших производных).

Метод понижения порядка: замена неизвестной функции

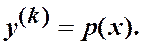
Þ

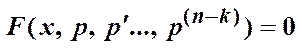
(д.у. (n – k)-го порядка)

Если удастся получить общее решение

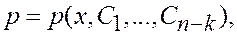
то затем решается уравнение

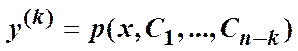
k -кратным интегрированием.

Пример. .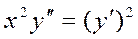

Решение. 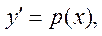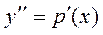Þ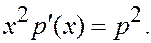

Это д.у. с разделяющимися переменными.

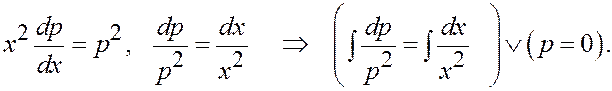
В первом случае:

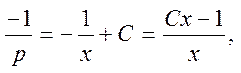
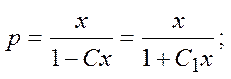
возвращаемся к y (x):

– при C ₁ ¹0

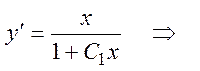
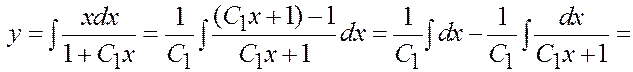
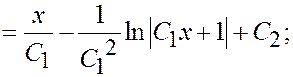
– при C ₁ = 0

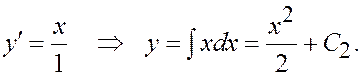
Во втором случае: y ¢= 0 Þ y = const.