2014-01-25
738
в приближённых вычислениях
Пример 1. Вычислить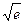 
с точностью до 0,001.
Решение. Задача состоит в вычислении функции ех при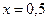 
. Используем разложение (9) для экспоненты, подставив туда х = 1 / 2:
.
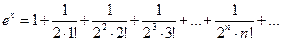Отбросив все члены, начиная с (n +1)-го, получим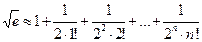 
. Погрешность этого приближённого равенства определяется суммой отброшенных членов (его n -го остатка):
.
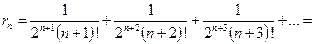
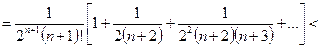
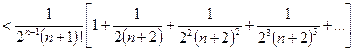В квадратных скобках стоит бесконечная сумма членов убывающей геометрической прогрессии, которую можно посчитать по формуле (2):
,
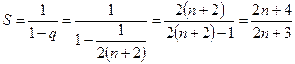и остаток ряда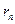 
< 
.
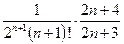Найдем такое n, при котором < 0,001, путём подбора:
n = 1: <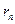
;
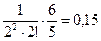n = 2: <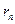
;
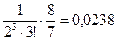n = 3: <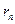
;
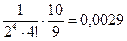n = 4: <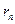
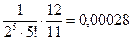< 0,001.
Итак, если ограничиться первыми пятью членами, то получим ответ:
.
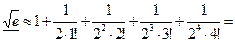
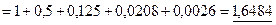Пример 2. Вычислить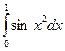 
с точностью до 0,001.
Решение. Запишем разложение функции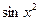 
в степенной ряд, воспользовавшись формулой (10):
.
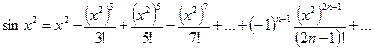По свойству степенных рядов полученный ряд можно интегрировать:
.
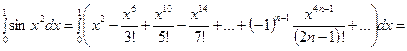
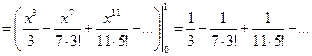Получим сходящийся знакочередующийся ряд, поскольку он удовлетворяет условиям теоремы Лейбница. Согласно следствию из этого признака сумма остатка ряда не превосходит по абсолютной величине первого члена остатка. Поэтому для вычисления с требуемой точностью нужно найти член ряда, который меньше заданной точности и, начиная с него, отбросить все остальные члены ряда. Третий член полученного ряда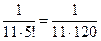 
< 0,001, и поэтому для вычисления с требуемой точностью достаточно взять первые два члена ряда:
.
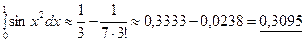Пример 3. Найти четыре первых члена разложения в степенной ряд решения дифференциального уравнения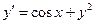 
, удовлетворяющего начальному условию 
.
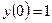Решение. Пусть искомое решение в окрестности т. х = 0 разложено в ряд Маклорена:
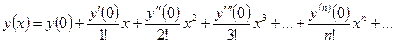
Найдем коэффициенты ряда:
1) 
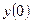= 1 (по условию задачи);
2) 
;
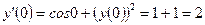3) 
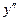найдём, дифференцируя данное уравнение:
=
, 
;
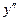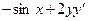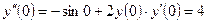4) Продифференцируем :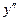
.
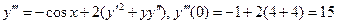Получим искомое частное решение данного уравнения: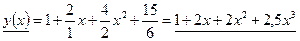 
.
Пример 4. Найти четыре первых члена разложения в степенной ряд решения дифференциального уравнения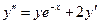 
, удовлетворяющего начальным условиям: 
.
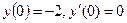Решение. Это уравнение линейное относительно у. Поэтому его можно решать и по-другому. Запишем решение не в виде ряда Маклорена, а как обычный степенной ряд, т.е.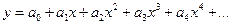 
. Здесь пока неизвестно, сколько слагаемых нужно написать, поскольку некоторые коэффициенты могут оказаться равными нулю. Поэтому выпишем члены разложения вплоть до третьей степени х.
Найдём две первые производные:
;
.
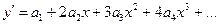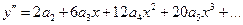Подставим получившиеся ряды в исходное уравнение, используя формулу (9), в которой х заменим на - х:
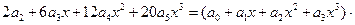
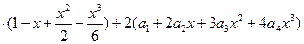Þ
.
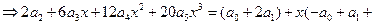
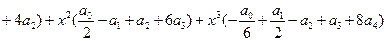А далее поступаем как всегда, т.е. приравниваем коэффициенты при одинаковых степенях х справа и слева, но предварительно используя начальные условия:
.
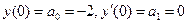Это будут «затравочные» коэффициенты, используя которые мы вычислим все остальные. В результате получим систему уравнений
.
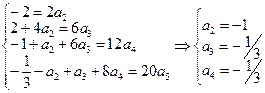Окончательный ответ таков:
.
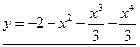Оказалось, что первоначально мы взяли лишний член ряда с х 3.
