Первая теорема двойственности
К контрольной работе
К началу К следующей лекции
К содержанию К титулу
Связь между оптимальными решениями двойственных задач устанавливается с помощью теорем двойственности.
Если 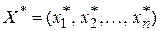 и
и 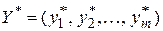 – допустимые решения взаимно двойственных задач, для которых выполняется равенство
– допустимые решения взаимно двойственных задач, для которых выполняется равенство
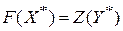 ,
,
то 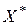 – оптимальное решение исходной задачи I, а
– оптимальное решение исходной задачи I, а 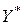 – двойственной задачи II.
– двойственной задачи II.
Кроме достаточного признака оптимальности взаимно двойственных задач существуют и другие важные соотношения междуих решениями. Прежде всего возникают вопросы: всегда ли для каждой пары двойственных задач есть одновременно оптимальные решения; возможна ли ситуация, когда одна из двойственных задач имеет решение, а другая нет. Ответ на эти вопросы дает следующая теорема.
Первая (основная) теорема двойственности. Если одна из взаимно двойственных задач имеет оптимальное решение, то его имеет и другая, причем оптимальные значения их линейных функций равны:
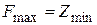 или
или 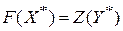 .
.
Если линейная функция одной из задач не ограничена, то условия другой задачи противоречивы (задача не имеет решения).
Замечание. Утверждение, обратное по отношению ко второй части основной теоремы двойственности, в общем случае неверно, т.е. из того, что условия исходной задачи противоречивы, не следует, что линейная функция двойственной задачи не ограничена.
Экономический смысл первой теоремы двойственности.
План производства 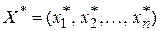 и набор цен (оценок) ресурсов
и набор цен (оценок) ресурсов 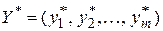 оказываются оптимальными тогда и только тогда, когда прибыль (выручка) от продукции, найденная при "внешних" (известных заранее) ценах
оказываются оптимальными тогда и только тогда, когда прибыль (выручка) от продукции, найденная при "внешних" (известных заранее) ценах 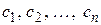 , равна затратам на ресурсы по "внутренним " (определяемым только из решения задачи) ценам
, равна затратам на ресурсы по "внутренним " (определяемым только из решения задачи) ценам 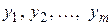 . Для всех же других планов Х и Y обеих задач прибыль (выручка) от продукции всегда меньше (или равна) затрат на ресурсы.
. Для всех же других планов Х и Y обеих задач прибыль (выручка) от продукции всегда меньше (или равна) затрат на ресурсы.
Экономический смысл первой теоремы двойственности можно интерпретировать и так: предприятию безразлично, производить ли продукцию по оптимальному плану 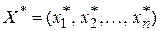 и получить максимальную прибыль (выручку)
и получить максимальную прибыль (выручку) 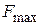 либо продавать ресурсы по оптимальным ценам
либо продавать ресурсы по оптимальным ценам 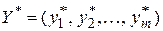 и возместить от продажи равные ей минимальные затраты на ресурсы
и возместить от продажи равные ей минимальные затраты на ресурсы 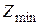 .
.
 2014-01-25
2014-01-25 804
804







