Точность представления чисел

Cтандарт IEEE

Мини ЭВМ

MF

S = 16, d = 64 – смещение порядка.

±

характеристика

мантисса

0 1 7 8 31

Характеристика: 0 ≤ X_A ≤ 127;

Порядок: -64 ≤ P_A ≤ 63.

1/16 • 16^-64 ≤ ‌‌‌‌‌‌‌‌| A_{п.т. норм} ‌‌‌‌‌‌‌‌| ≤ 1 • 16⁶³

S = 2; d = 128 – смещение порядка.

31 23 22 0

Характеристика: 0 ≤ X_A ≤ 225;

Порядок: -128 ≤ P_A ≤ 127.

1/2 • 2^-128 ≤ ‌‌‌‌‌‌‌‌| A_{п.т. норм} ‌‌‌‌‌‌‌‌| ≤ 1 • 2¹²⁷

S = 2;

d = 127 – для короткого формата;

d = 1023 – для длинного формата;

d = 16383 – для расширенного формата.

31 23 22 0

характеристика мантисса

Скрытая единица имеется только в коротком или длинном формате, в расширенном формате она представляется в явном виде.

При определении диапазона представления чисел необходимо учитывать особенности стандарта IEEE-754:

Крайние значение характеристики (порядка) во всех форматах зарезервированы и для представления нормализованных чисел не используются. Максимальное значение характеристики при знаке + и нулевой мантиссе зарезервировано для +∞ и для представления не чисел (NAN). Максимальное значение характеристики с единицей в старшем разряде мантиссы используется для представления -∞. Минимальное значение характеристики используется для представления ненормализованных чисел со знаками +,- и для представления нуля(+0 и -0).

Поэтому диапазон характеристики

для короткого формата: 1 ≤X_A ≤ 254;

диапазон чисел: 2^-126 ≤ ‌‌‌‌‌‌‌‌| A_{п.т. норм} ‌‌‌‌‌‌‌‌| < 2¹²⁸.

для длинного формата:10^-308 ≤ ‌‌‌‌‌‌‌‌| A_{п.т. норм} ‌‌‌‌‌‌‌‌| < 10³⁰⁸.

для расширенного формата:10^-4932 ≤ ‌‌‌‌‌‌‌‌| A_{п.т. норм} ‌‌‌‌‌‌‌‌| < 10⁴⁹³²

Практически каждая конечная десятичная дробь представляется в виде бесконечной двоичной дроби, что в условиях ограниченного формата приводит к возникновению погрешности.

Точность представления чисел с плавающей запятой принято характеризовать максимальным значением относительной погрешности.

Максимальная абсолютная погрешность дробного числа имеет место в том случае, когда все отбрасываемые разряды равны единице.

_____A_____ A^*

0. 10 ………110. 111 …….1

n n+1 ∞

Значение максимальной погрешности:

∞

Δ А_др.max = ∑ 2^-i = 2^-n, (n- разрядность дробного числа) совпадает с

i=n+1

весом младшего разряда формата.

Относительная погрешность дробных чисел:

δ А_др.min =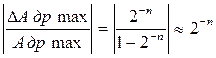

δ А_др.max =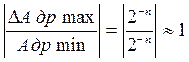

Погрешность представления чисел с плавающей точкой определяется погрешностью мантиссы как дробного числа.

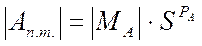
δ А_{п.т. =}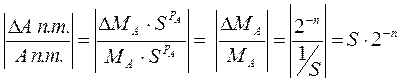

Формула справедлива для правильных и неправильных дробей.

Точность представления чисел для различных типов ЭВМ

1. ЕС: δ А_п.т. = 16 • 2^-24 = 2^-20 = 10^-6;

2. СМ: δ А_п.т. = 2 • 2^-24 = 2^-23 = 10^-7;

3. ПК: δ А_п.т. = 10^-7.

Методы округления чисел с плавающей точкой

Округление производится для повышения точности представления чисел.

Методы округления оговариваются стандартом IEEE 754.

• Округление усечением – не вписывающиеся в сетку разряды отбрасываются;

• Округление к ближайшему – анализируется старший отбрасываемый разряд, если он равен 1, то к младшему разряду мантиссы добавляется единица;

• Округление к ближайшему большему (к +∞) - для положительных чисел в младший разряд мантиссы добавляется единица, для отрицательных чисел мантисса не меняется.

• Округление к ближайшему меньшему (к -∞) – для отрицательных чисел в младший разряд мантиссы добавляется единица, для положительных чисел мантисса не меняется.

.

Все методы, кроме усечения, позволяют уменьшить максимальную относительную погрешность. По умолчанию используется метод округления к ближайшему.