Примеры сходящихся и расходящихся рядов

Понятие суммы ряда

Пусть числовой ряд 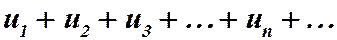(3)

сходится. Это значит, по определению, что последовательность его частичных сумм 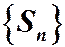имеет конечный предел. Обозначим его через S: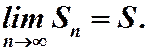

Число S называется суммой ряда (3). Можно записать: .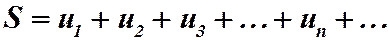

Пример 5. Пусть дан ряд: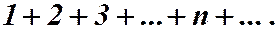

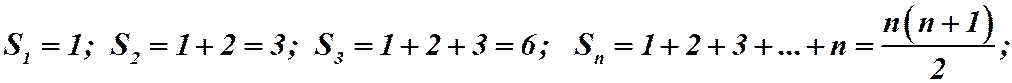
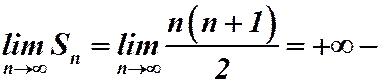ряд расходится.

Пример 6. Имеем ряд:

Не трудно проверить, что

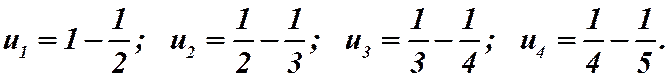
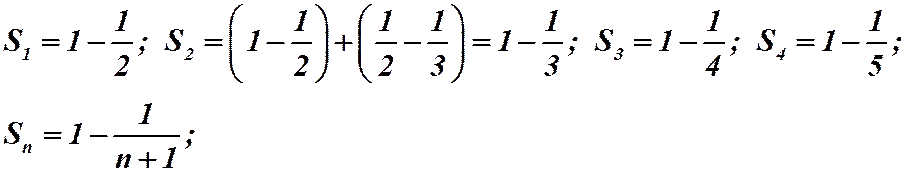
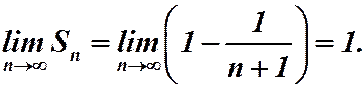Ряд сходится и его сумма равна 1.

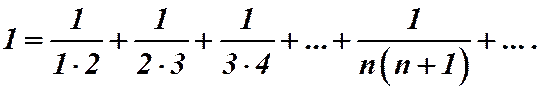
Пример 7. Дан гармонический ряд: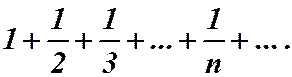

Запишем п - ю частичную сумму: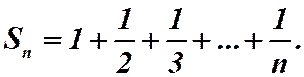

Докажем, что гармонический ряд расходится. Из теории пределов известно, что последовательность с общим членом имеет конечный предел, равный е. (Второй замечательный предел).

При этом известно, что эта последовательность строго возрастает, значит, при любом п имеем:

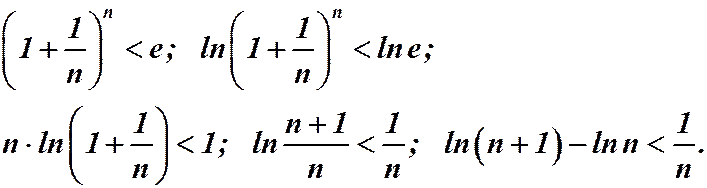
Запишем неравенство при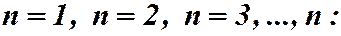

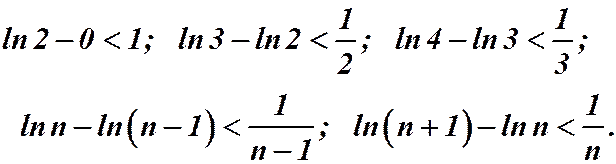
Складывая почленно неравенства, получим:

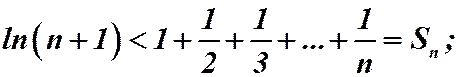
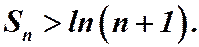
Переходя к пределу при 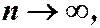получим: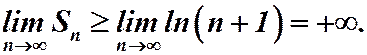

Значит, 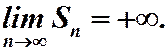Гармонический ряд расходится.

Пример 8. Исследовать на сходимость ряд: 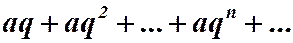(4)

п - ая частичная сумма 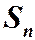есть сумма первых п членов геометрической прогрессии и, как известно, 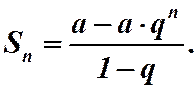Рассмотрим случаи:

1) Пусть 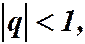тогда 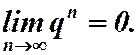Значит,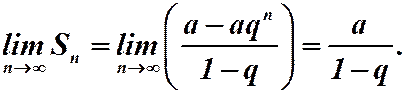

Ряд сходится и его сумма равна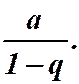

2) Пусть 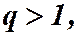тогда 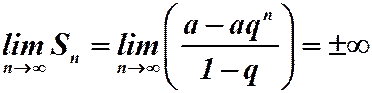(в зависимости от а).

Ряд расходится.

3) Пусть 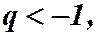тогда 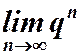не существует. Ряд расходится.

4) Пусть 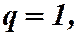тогда .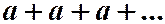

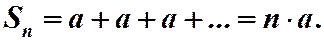
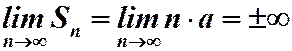(в зависимости от а). Ряд расходится.

5) Пусть 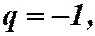тогда 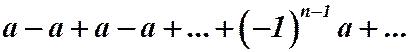. Последовательность частичных сумм предела не имеет, т.к.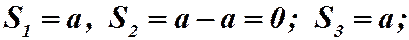

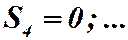
Итак, если 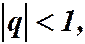то ряд (4) сходится; если 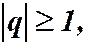то ряд (4) расходится.