Необходимый признак сходимости ряда

Теорема 1. Если числовой ряд сходится, то предел его п - го члена при 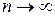равен 0.

Доказательство. Пусть числовой ряд 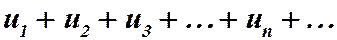(5)

сходится. Требуется доказать, что предел 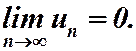Запишем п - ю и 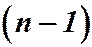- ю частичные суммы ряда (5):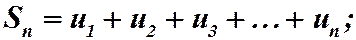

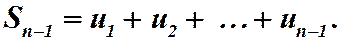
Вычитая почленно из первого равенства второе, найдем: 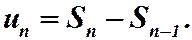(6)

По условию теоремы ряд (5) сходится. Обозначим его сумму через S. Тогда 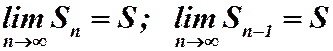. Переходя к пределу в (6), имеем: 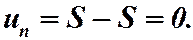Теорема доказана.

Замечание 2. Теорема не является достаточным признаком сходимости ряда, то есть если для какого-нибудь ряда 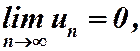то это не значит, что ряд сходится. Например, гармонический ряд 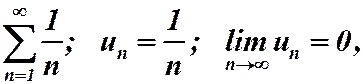но он расходится.