Ряды с произвольными членами

Определение 6. Числовой ряд 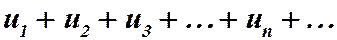(22)

называется рядом с произвольными членами, если в нем имеется бесконечное множество положительных членов и бесконечное множество отрицательных членов.

Частным видом ряда с произвольными членами является ряд со знакочередующимися членами.

Определение 7. Числовой ряд (22) называется абсолютно сходящимся, если сходится ряд, составленный из модулей членов этого ряда: 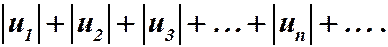(23)

Пусть ряд (22) сходится абсолютно, это значит, по определению, что сходится ряд (23). Возникает вопрос, а сходится ли сам ряд (22)? Ответ дает теорема.

Теорема 15. Абсолютно сходящийся ряд есть ряд сходящийся.

Определение 8. Числовой ряд (22) называется не абсолютно сходящимся, если он сходится, а ряд, составленный из модулей его членов, т.е. ряд (23) расходится. Не абсолютно сходящийся ряд называется условно сходящимся.

Пример 16.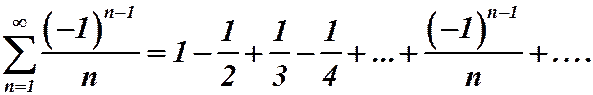

Решение. Этот ряд со знакочередующимися членами, его члены убывают по модулю, и 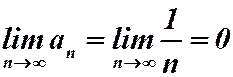. Ряд сходится по теореме Лейбница. Запишем ряд, состоящий из модулей: 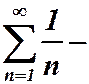гармонический ряд. Он расходится. Следовательно, исходный ряд сходится условно.

Пример 17.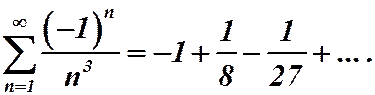

Решение. Этот ряд со знакочередующимися членами. Он сходится по теореме Лейбница. Запишем ряд, состоящий из модулей: 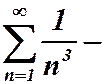обобщенный гармонический ряд. Он сходится при 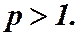Значит, исходный ряд сходится абсолютно.