Регрессия

Корреляционно – регрессионный анализ. Линейная парная

Корреляционно-регрессионный анализ включает в себя измерение тесноты, направление связи и установление аналитического выражения связи.

Одним из методов корреляционно-регрессионного анализа является метод парной корреляции, рассматривающий влияние вариации факторного признака Х на результативный У. Аналитическая связь между ними описывается уравнениями:

прямой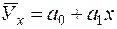

параболы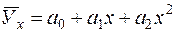

гиперболы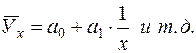

Если результативный и факторный признаки возрастают одинаково, примерно в арифметической прогрессии, то это свидетельствует о наличии линейной связи между ними, а при обратной связи – гиперболической. Если результативный признак увеличивается в арифметической прогрессии, а факторный значительно быстрее, то используется параболическая или степенная функции.

Оценка параметров уравнения регрессии а_о и а₁ осуществляется методом наименьших квадратов, в основе которого лежит требование минимальности сумм квадратов отклонений эмпирических данных Y_i от выровненных (теоретических) :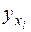

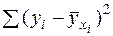à min (1)

Система нормальных уравнений для нахождения параметров линейной парной регрессии имеет вид:

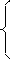
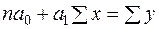(2)

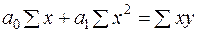
Для оценки типичности параметров уравнения регрессии используется
t – критерий Стьюдента. При этом вычисляются значения t - критерия:

для параметра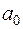

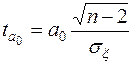(3)

для параметра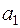

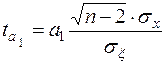(4)

В формулах (3) и (4):

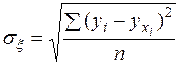(5)

σ_ξ - среднее квадратическое отклонение результативного признака 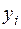от выровненных значений :

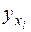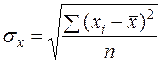(6)

σ_X - среднее квадратическое отклонение факторного признака 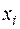от общей средней .

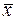Полученные по формулам (3) и (4) фактические значения 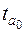и 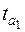сравниваются с критическим 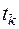, который получают по таблице Стьюдента с учетом принятого уровня значимости 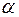и числа степеней свободы .

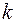Полученные при анализе корреляционной связи параметры уравнения регрессии признаются типичными, если t фактическое больше t критического

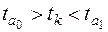(7)

По проверенным на типичность параметрам уравнения регрессии производится построение математической модели связи. При этом параметры примененной в анализе математической функции получают соответствующие количественные значения: параметр а ₀ показывает усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов; параметр а ₁ – на сколько изменяется в среднем значение результативного признака при изменении факторного на единицу его собственного измерения.

Проверка практической значимости синтезированных в корреляционно-регрессивном анализе математических моделей осуществляется посредством показателей тесноты связи между признаками х и у.

Для статистической оценки тесноты связи применяются следующие показатели вариации:

1) общая дисперсия результативного признака 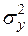, отображающая общее влияние всех факторов

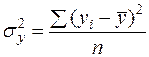(8)

2) факторная дисперсия результативного признака 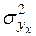, отражающая вариацию y только от воздействия изучаемого фактора x

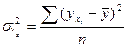(9)

Формула (9) характеризует отклонение выровненных значений 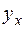от их общей средней величины ;

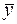3) остаточная дисперсия 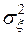, отражающая вариацию результативного признака y от всех прочих, кроме x, факторов

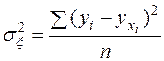(10)

Формула (10) характеризует отклонения эмпирических (фактических) значений результативного признака y_i от их выровненных значений .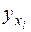

Соотношение между факторной и общей дисперсиями характеризует меру тесноты связи между признаками x и y

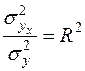(11)

Показатель R² называется индексом детерминации (причинности). Он выражает долю факторной дисперсии, т.е. характеризует, какая часть общей вариации результативного признака y объясняется изменением факторного признака x.

На основе формулы (11) определяется индекс корреляции R

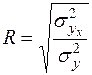(12)

Используя правило сложения дисперсии, получают формулу индекса корреляции

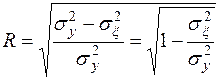(13)

Формула (71) является основным алгоритмом для определения индекса корреляции с использованием машинной обработки анализируемых данных.

При прямолинейной форме связи показатель тесноты связи определяется по формуле линейного коэффициента корреляции r.

В теории разработаны и на практике применяются различные модификации формулы расчёта данного коэффициента:

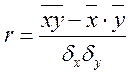, где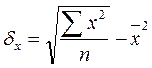

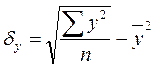
или

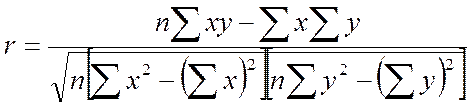
или 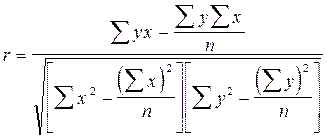(14)

Заметим, что по абсолютной величине линейный коэффициент корреляции r равен индексу корреляции r только при прямолинейной связи.

Линейный коэффициент корреляции изменяется в пределах от -1 до 1: -1 ≤ r ≤ 1. Знаки коэффициентов регрессии корреляции совпадают. При этом интерпретацию выходных значений коэффициента корреляции можно представить в следующей таблице: