Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными. Простая средняя считается по несгруппированным данным и имеет следующий общий вид:
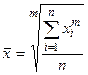
где x i - варианта (значение) осредняемого признака;
m - показатель степени средней;
n - число вариант.
Взвешенная средняя считается по сгруппированным данным и имеет общий вид
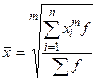
где x i - варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта;
m - показатель степени средней;
f i - частота, показывающая, сколько раз встречается i - е значение осредняемого признака.
Общие формулы расчета степенных средних имеют показатель степени (m). В зависимости от того, какое значение он принимает, различают следующие виды степенных средних (простых и взвешенных):
средняя гармоническая, если m = -1
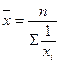
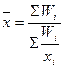
средняя геометрическая, если m ® 0
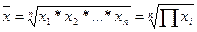
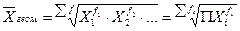
средняя арифметическая, если m = 1
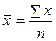
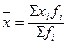
средняя квадратическая, если m =2
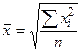
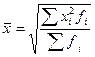
средняя кубическая, если m =3
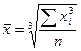
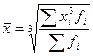
В статистической практике чаще, чем остальные виды средних используются средние арифметические средние гармонические.
Порядок выбора формы средней качественного признака основан на следующих правилах:
1. Если имеется ряд данных по двум взаимосвязанным показателям, для одного из которых нужно вычислить среднюю величину, и при этом известны численные значения знаменателя ее логической формулы, а значения числителя не известны, но могут быть найдены как произведения этих показателей, то средняя должна вычисляться по формуле средней арифметической.
2. Если в указанной постановке задачи известны численные значения числителя логической формулы, а значения знаменателя не известны, но могут быть найдены как частное от деления одного показателя на другой, то средняя вычисляться по формуле средней гармонической.
3. В том случае, когда в условии задачи даны численные значения числителя и знаменателя логической формулы показателя, средняя вычисляется непосредственно по этой формуле.
Любая средняя величина должна вычисляться так, чтобы при замене ею каждого варианта осредняемого признака не изменялась величина итогового, обобщающего показателя, который связан с осредняемым показателем.
При использовании взвешенных средних нужно иметь в виду, что понятие вес и частота в общем случае не совпадают, не являются тождественными. При выборе взвешивающего показателя следует учитывать, что при умножении варианты на вес (в случае использования формулы средней арифметической) или при делении объемного показателя на вес (в случае использования формулы средней гармонической) должна получиться реальная экономическая величина.
 2014-01-25
2014-01-25 726
726








