Основная задача выборочного наблюдения в экономике состоит в том, чтобы на основе характеристик выборочной совокупности (средней и доли) получить достоверные суждения о показателях средней и доли в генеральной совокупности. При этом следует иметь в виду, что при любых статистических исследованиях (сплошных и выборочных) возникают ошибки двух видов: регистрации и репрезентативности.
Ошибки регистрации могут иметь случайный (непреднамеренный) и систематический (тенденциозный) характер. Случайные ошибки обычно уравновешивают друг друга, поскольку не имеют преимущественного направления в сторону преувеличения или преуменьшения значения изучаемого показателя. Систематические ошибки направлены в одну сторону вследствие преднамеренного нарушения правил отбора (предвзятые цели). Их можно избежать при правильной организации и проведения наблюдения.
Ошибки репрезентативности присущи только выборочному наблюдению и возникают в силу того, что выборочная совокупность не полностью воспроизводит генеральную. Они представляют собой расхождение между значениями показателей, полученных по выборке, и значениями показателей этих же величин, которые были бы получены при проведенном с одинаковой степенью точности сплошном наблюдении, т.е. между величинами выборных и соответствующих генеральных показателей.
Ошибки репрезентативности могут быть систематическими и случайными. Систематические ошибки возникают при нарушении установленных правил отбора единиц. Случайные ошибки репрезентативности обязаны своим возникновением недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности.
Величина случайной ошибки определяет надежность данных выборочного наблюдения, их пригодность для суждения о генеральной совокупности.
Величина случайной ошибки репрезентативности зависит от:
· степени колеблемости изучаемого признака в генеральной совокупности;
· способа формирования выборочной совокупности;
· объема выборки.
Для каждого конкретного выборочного наблюдения значение ошибки репрезентативности может быть определено по соответствующим формулам, которые зависят от вида, метода и способа формирования выборочной совокупности.
Формула определения средней ошибки выборки для средней величины (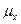 ) определяется следующим образом:
) определяется следующим образом:
при повторном отборе:
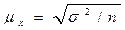 ,
,
при бесповторном отборе:
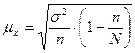 ,
,
где n – численность выборки; N – численность генеральной совокупности.
Величина (1 – n / N) всегда меньше единицы, поэтому сопоставление приведенных формул свидетельствует о том, что применение бесповторного отбора обеспечивает меньшую ошибку выборки.
Таким образом, формулы для расчета средней ошибки выборочной доли имеют вид:
для повторного отбора
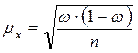 ,
,
безповторного отбора
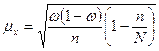 .
.
Приведенные формулы характеризуют среднюю величину отклонения сводных характеристик генеральной совокупности. Однако то, что генеральная средняя (или генеральная доля) не выйдет за определенные пределы, можно утверждать не с абсолютной достоверностью, а лишь с определенной степенью вероятности. Доказано, что генеральные характеристики не отклоняются от выборочных на величину большую, чем величина ошибки выборки, и всегда имеют степень вероятности, равную 0,683. Т.е. из 1000 выборок в 683 выборках сводная характеристика генеральной совокупности будет отличаться от сводной характеристики выборочной совокупности не более чем на величину, равную 1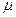 ; но в остальных 317 выборках из 1000 она может отличаться и в большей степени.
; но в остальных 317 выборках из 1000 она может отличаться и в большей степени.
Можно повысить вероятность этого утверждения, если расширить пределы отклонений, приняв в качестве меры, удвоенную ошибку выборки - 2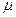 . В этом случае вероятность нашего утверждения достигнет уже 0,954, т.е. только в 46 выборках из 1000 отклонение выйдет за пределы 2
. В этом случае вероятность нашего утверждения достигнет уже 0,954, т.е. только в 46 выборках из 1000 отклонение выйдет за пределы 2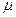 . При 3
. При 3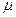 вероятность соответственно повышается до 0,997, и таким образом она все более и более приближается к 1. Таким образом, проявление ошибки большей, чем утроенная средняя ошибка выборки, имеет крайне малую вероятность (1-0,997=0,003) и считается практически невозможным событием. С определенной степенью вероятности можно утверждать, что отклонения выборочных характеристик от генеральных не превысят некоторой величины, которая называется предельной ошибкой выборки.
вероятность соответственно повышается до 0,997, и таким образом она все более и более приближается к 1. Таким образом, проявление ошибки большей, чем утроенная средняя ошибка выборки, имеет крайне малую вероятность (1-0,997=0,003) и считается практически невозможным событием. С определенной степенью вероятности можно утверждать, что отклонения выборочных характеристик от генеральных не превысят некоторой величины, которая называется предельной ошибкой выборки.
Придельная ошибка выборки (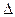 ) связана со средней ошибкой выборки следующим равенством:
) связана со средней ошибкой выборки следующим равенством:
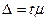 ,
,
где t – коэффициент доверия,зависящий от вероятности, с которой можно гарантровать, что предельная ошибка не превысит t-кратную среднюю ошибку. Этот коэффициент определяется по таблице значений интегральной функции Лапласа при заданной доверительной вероятности.
Способы распространения выборочных данных на генеральную совокупность. Зная величину выборочной средней (x) или доли (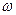 ), а также предельную ошибку выборки (
), а также предельную ошибку выборки (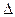 ), можно определить доверительные интервалы, в которых находятся значения генеральных параметров:
), можно определить доверительные интервалы, в которых находятся значения генеральных параметров:
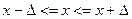 ,
,
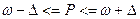 .
.
 2014-01-25
2014-01-25 1000
1000







