Под элементом электрической сети понимают участок (звено) ее схемы замещения, например, линии электропередачи или трансформатора (рис. 4.3). Так, в случае линии электропередачи звеном будет являться участок ее П-образной схемы замещения между проводимостями. Поскольку в звене сети присутствует только сопротивление Z=R+jX, ток в начале и в конце звена остается неизменным. Расчет будем вести в линейных напряжениях.
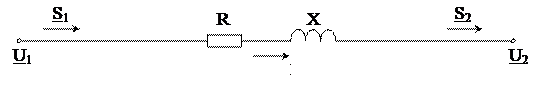 |
| Схема замещения элемента электрической сети |
Рассмотрим наиболее характерные для практики случаи.
Случай 1 (Расчет по данным конца): известны мощность и напряжение в конце звена: S 2=P2 - jQ2; U 2. Требуется определить мощность S 1 и напряжение U 1 в начале.
Этот случай встречается в практике, например, если задана нагрузка потребителя и требуется найти напряжение источника питания, при котором будет обеспечено требуемое напряжение у потребителя.
Потери мощности определим по данным конца звена:
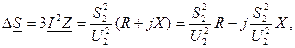 |
т.е. потери активной мощности:
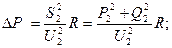 |
потери реактивной мощности:
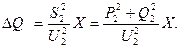 |
Мощность в начале звена:
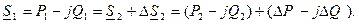 |
В этом случае потокораспределение находится точно, т.к. мощность и напряжение заданы в одной точке (в конце).
Совмещая вектор напряжения U 2 с вещественной осью, запишем:
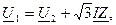 |
Тогда:
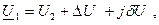 |
где продольная составляющая падения напряжения:
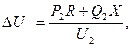 |
поперечная составляющая падения напряжения:
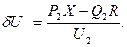 |
Модуль напряжения в начале звена определяется по выражению (4.15).
Векторная диаграмма напряжений для этого случая показана на рис. 4.4, а.
Случай 2 (Расчет по данным начала): известны мощность и напряжение в начале звена: S 1=P1- jQ1; U 1. Требуется определить мощность S 2 и напряжение U 2 в конце. На практике этот случай имеет место тогда, когда возникает необходимость передачи заданной мощности источника (электростанции) при фиксированном напряжении на его шинах в центр потребления. При этом следует выяснить, каково будет напряжение у потребителей.
Потери мощности, выраженные через параметры начала:
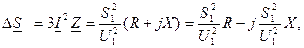 |
т.е.
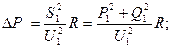 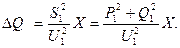 |
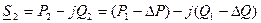 |
В этом случае потокораспределение также находится точно, т.к. мощность и напряжение заданы в одной точке (в начале).
Совмещая вектор напряжения U 1 с вещественной осью, запишем:
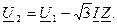 |
Тогда:
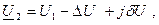 |
где продольная составляющая падения напряжения:
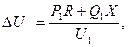 |
поперечная составляющая падения напряжения:
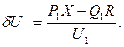 |
Модуль напряжения в конце звена определяется по выражению (4.16).
Векторная диаграмма напряжений для этого случая показана на рис. 4.4, б.
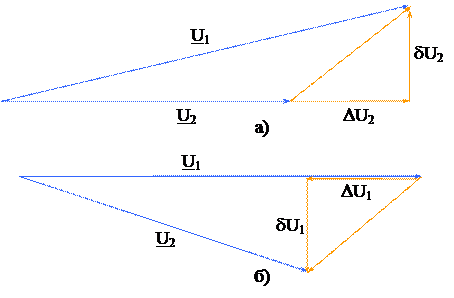 |
| Векторные диаграммы для звена сети: а – по данным конца; б – по данным начала |
Случай 3: известны мощность в конце звена S 2=P2 - jQ2 и напряжение в начале U 1. Требуется найти мощность в начале звена S 1=P1- jQ1 и напряжение в конце U 2. Этот случай наиболее типичный, так как обычно известно напряжение на шинах источника питания (электростанции, понижающей подстанции), от которого отходят линии с заданными нагрузками потребителей в конце.
Здесь сразу вычислить напряжение U 2 не представляется возможным, так как не известна мощность в начале звена. Поэтому расчет ведут методом последовательных приближений напряжения 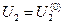 . Если нет никаких соображений по выбору величины
. Если нет никаких соображений по выбору величины 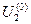 , то ее принимают равной номинальному напряжению сети. Тогда, зная
, то ее принимают равной номинальному напряжению сети. Тогда, зная 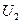 , можно найти первое приближение мощности в начале звена:
, можно найти первое приближение мощности в начале звена:
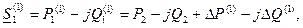 |
где потери мощности определяют как:
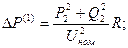 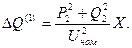 |
Теперь можно найти первое приближение напряжения:
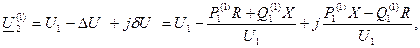 |
модуль которого подставляют в формулу (4.33) для вычисления потерь мощности и снова находят мощность в начале звена (второе приближение). Расчет заканчивают в том случае, если разность между модулями напряжений U2 i-го и (i-1)-го приближений не больше заданной точности расчета:
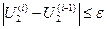 . . |
При расчетах без применения ЭВМ обычно ограничиваются расчетом первого приближения напряжения 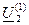 и мощности
и мощности 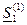 .
.
 2014-01-25
2014-01-25 4464
4464








