Геометрическое место мгновенных центров скоростей, отмеченных на неподвижной плоскости, называется неподвижной центроидой.
При качении цилиндра по горизонтальной плоскости (рис. 5.8 д) неподвижная центроида – горизонтальная прямая, а подвижная – окружность.
В каждый момент времени подвижная и неподвижная центроиды имеют общую точку касания – мгновенный центр скоростей Р, т.е. точку, скорость которой равна нулю. Поэтому плоское движение можно представить, как качение без скольжения подвижной центроиды по неподвижной.
5.4. Ускорения точек при плоском движении.
Мгновенный центр ускорений
Для определения ускорения точки плоской фигуры продифференцируем равенство (5.5) по времени:
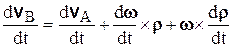 .
.
В этом соотношении 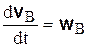 ,
, 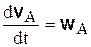 – соответственно ускорения точек В и А,
– соответственно ускорения точек В и А, 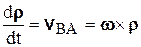 ,
, 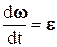 – вектор углового ускорения. Таким образом, ускорения точек А и В связаны между собой соотношением
– вектор углового ускорения. Таким образом, ускорения точек А и В связаны между собой соотношением
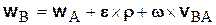 . (5.7)
. (5.7)
Два последних слагаемых в равенстве (5.7) определяют ускорение точки В при закрепленной точке А 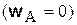 . Поэтому их сумма
. Поэтому их сумма
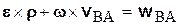
дает ускорение точки В во вращательном движении относительно системы координат Ах2у2.
При изучении вращательного движения мы уже выяснили, как направлены составляющие вектора ускорения 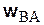 . Сохраним за этими составляющими старые названия – осестремительного (или центростремительного) и вращательного ускорений, т.е.
. Сохраним за этими составляющими старые названия – осестремительного (или центростремительного) и вращательного ускорений, т.е.
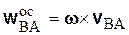 ,
, 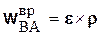 .
.
Модули этих составляющих будут
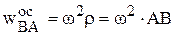 ,
, 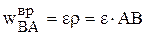 . (5.8)
. (5.8)
На рис. 5.9 геометрически сложены три вектора и определено ускорение точки В при помощи формулы
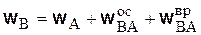 . (5.9)
. (5.9)
 2014-01-25
2014-01-25 723
723








