Движение твердого тела с одной неподвижной точкой. Свободное твердое тело

Таким образом, ускорение любой точки В плоской фигуры геометрически складывается из ускорения полюса и осестремительного и вращательного ускорений во вращательном движении фигуры относительно полюса.

Заметим, что при решении задач, прежде чем определить ускорение точки по формуле (5.9), необходимо вычислить угловую скорость тела, его угловое ускорение и выбрать полюс. За полюс выбирается обычно такая точка, ускорение которой легко находится из условия задачи. Иногда, зная, например, направление искомого ускорения точки, угловое ускорение можно определить по формуле (5.9).

Из (5.8) найдем угол между вектором 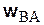и направлением на полюс (рис. 5.9),

.

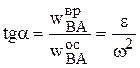Отсюда видно, что этот угол, во-первых, не зависит от выбора полюса и, во-вторых, для всех точек при фиксированном времени одинаков.

Модуль ускорения точки при вращении фигуры вокруг полюса также находится из равенства (5.8)

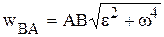. (5.10)

Он зависит от расстояния точки до полюса.

Введем понятие мгновенного центра ускорений.

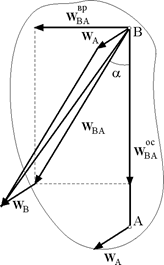Рис. 5.9.

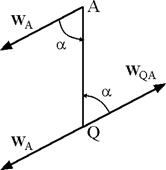Рис. 5.10.

Мгновенным центром ускорений называется точка плоской фигуры, ускорение которой в данный момент времени равно нулю. Для построения мгновенного центра ускорений будем предполагать, что нам известны ускорение одной из точек 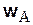, угловая скорость 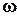и угловое ускорение 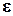, причем предполагается, что 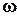и 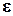не равны нулю одновременно. Из точки А отложим под углом 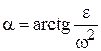к ускорению 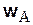отрезок AQ

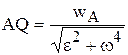. (5.11)

При 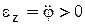угол откладывается против хода часовой стрелки (рис. 5.10), при 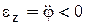– по ходу часовой стрелки.

Убедимся в том, что ускорение точки Q равно нулю. Выбрав за полюс точку А, получим

.

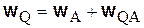Как мы уже отметили ранее, угол между ускорением точки относительно полюса и направлением на полюс не зависит от выбора полюса. Следовательно, 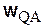составляет с направлением QA угол 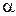. Такой же угол составляет и 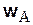с AQ. Поэтому векторы 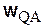и 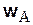параллельны (рис. 5.10). В силу принятого правила отсчета угла 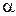ускорения 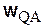и 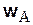будут всегда противоположно направлены. Остается теперь установить, что они равны по модулю. Вспоминая (5.10) и подставляя (5.11), получим

.

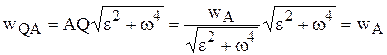Отсюда следует:

.

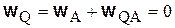Таким образом, мы доказали, что точка Q – мгновенный центр ускорений.

Ускорение любой точки в данный момент времени теперь может быть определено так же, как и при вращении вокруг неподвижной оси:

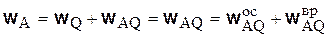
(поскольку ).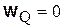

Следует иметь в виду, что мгновенный центр ускорений и мгновенный центр скоростей, – вообще говоря, разные точки. В этом легко убедиться, рассмотрев простой пример. Допустим, диск катится по горизонтальной плоскости без скольжения (рис. 5.8 д) и скорость его центра О постоянна. Как мы уже знаем, мгновенный центр скоростей находится в точке касания Р. Так как вектор скорости точки О постоянен, то ускорение центра диска равно нулю. Таким образом, мгновенный центр ускорений совпадает с центром диска, а мгновенный центр скоростей – с точкой касания.