Задание движения
ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
Плоским называется такое движение твердого тела, при котором все его точки перемещаются в плоскостях, параллельных некоторой неподвижной плоскости.
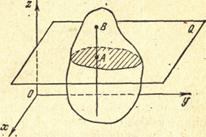
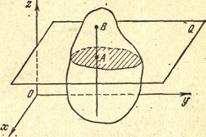
| Из определения плоского движения следует, что любая прямая АВ, проведенная в теле перпендикулярно плоскости ху, будет перемещаться поступательно, т.е. траектории, скорости и ускорения всех точек этой прямой будут одинаковы (рис. 5.1). | 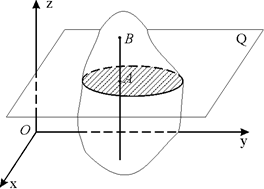 Рис. 5.1. Рис. 5.1. |
Таким образом, для определения движения тела необходимо знать движение лишь одной точки на каждой прямой, проведенной перпендикулярно плоскости ху. Взяв точки в одной плоскости, параллельной плоскости ху, мы можем утверждать, что плоское движение твердого тела вполне определяется движением плоской фигуры, полученной от пересечения тела любой плоскостью Q, параллельной плоскости ху (см. рис. 5.1). Следовательно, задание движения твердого тела сводится к заданию движения одного его сечения.
Рассмотрим две точки плоской фигуры А (х1А, ylA) и В (xlB, ylВ), находящейся в плоскости Ох1у1 (рис. 5.2 а). Так как расстояние 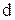 между этими точками остается неизменным
между этими точками остается неизменным
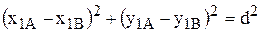 ,
,
то из четырех координат независимых только три. Таким образом, для описания плоского движения тела требуется знать три независимые координаты как функции времени.
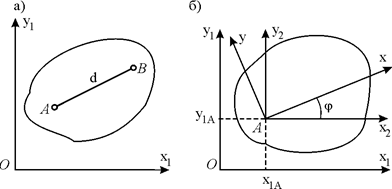 Рис. 5.2. Рис. 5.2. |
Свяжем жестко с плоской фигурой систему координат Аху. Тогда положение системы Аху, а вместе с ней и положение плоской фигуры относительно системы координат Ох1у1 будет вполне определено заданием координат xlA и ylA точки А и углом 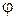 между осями Ах 2 и Ах – см. рис. 5.2 б (оси Ах 2 и Ay 2 соответственно параллельны осям Ох 1 и Оу 1 и перемещаются при движении фигуры поступательно). Следовательно, три функции времени
между осями Ах 2 и Ах – см. рис. 5.2 б (оси Ах 2 и Ay 2 соответственно параллельны осям Ох 1 и Оу 1 и перемещаются при движении фигуры поступательно). Следовательно, три функции времени
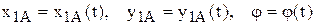 (5.1)
(5.1)
определяют положение плоской фигуры в любой момент времени. Равенства (5.1) называются уравнениями движения плоской фигуры или уравнениями плоского движения твердого тела.
 |
 |
Пусть система координат Ох1у1 является неподвижной системой, а система координат Ах 2 у 2, имеющая начало в произвольно выбранной точке А плоской фигуры, движется поступательно. Систему координат Аху жестко свяжем с плоской фигурой.
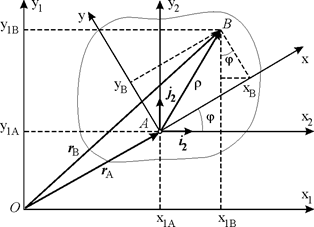 Рис. 5.3. Рис. 5.3. | Радиус-вектор 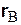 , определяющий положение точки В относительно неподвижной системы координат Ох 1 у 1 (рис. 5.3), можно задать при помощи двух векторов: , определяющий положение точки В относительно неподвижной системы координат Ох 1 у 1 (рис. 5.3), можно задать при помощи двух векторов: 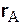 , определяющего положение точки А в системе отсчета Ох 1 у 1, и , определяющего положение точки А в системе отсчета Ох 1 у 1, и 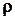 , , |
определяющего положение точки В в системе отсчета Ах 2 у 2,
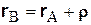 . (5.2)
. (5.2)
Дифференцируя (5.2) по времени, получим
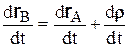 . (5.3)
. (5.3)
Заметим, что 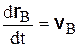 ,
, 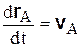 . Что же касается
. Что же касается 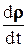 , то это есть скорость точки В относительно подвижной системы координат Ах 2 у 2, т.е. относительная скорость. Введем для нее обозначение
, то это есть скорость точки В относительно подвижной системы координат Ах 2 у 2, т.е. относительная скорость. Введем для нее обозначение 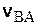 :
:
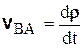 .
.
Движение тела относительно системы координат Ах 2 у 2 представляет собой вращение тела вокруг оси Аz 2, направленной перпендикулярно плоскости чертежа (рис. 5.3) на читателя. Таким образом, скорость 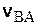 есть скорость точки В при вращении тела вокруг оси Аz 2. Для определения этой скорости мы уже получили формулу
есть скорость точки В при вращении тела вокруг оси Аz 2. Для определения этой скорости мы уже получили формулу
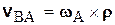 ,
,
где 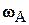 – угловая скорость вращения фигуры вокруг точки А (вокруг оси Аz 2), которую в дальнейшем будем называть полюсом. Формула (5.3) принимает теперь вид
– угловая скорость вращения фигуры вокруг точки А (вокруг оси Аz 2), которую в дальнейшем будем называть полюсом. Формула (5.3) принимает теперь вид
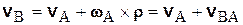 , (5.4)
, (5.4)
т.е. скорость какой-либо точки В плоской фигуры равна геометрической сумме скорости полюса А и скорости точки В при вращении плоской фигуры вокруг полюса А.
Покажем, что угловая скорость вращения фигуры не зависит от выбора полюса. Пусть А и В – две какие-нибудь точки плоской фигуры. Пусть полюсу А соответствует угловая скорость 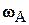 , а полюсу В – угловая скорость
, а полюсу В – угловая скорость 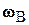 . Найдем скорость точки В, приняв за полюс точку А
. Найдем скорость точки В, приняв за полюс точку А
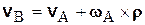 .
.
Приняв теперь за полюс точку В, найдем скорость точки А
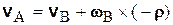 .
.
Сложив оба равенства, получим 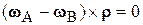 .
.
Но вектор 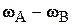 перпендикулярен плоскости фигуры, и, значит, полученное равенство может выполняться только при
перпендикулярен плоскости фигуры, и, значит, полученное равенство может выполняться только при 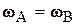 . Таким образом, нет надобности в дальнейшем сохранять индекс полюса в обозначении вектора угловой скорости, т.е.
. Таким образом, нет надобности в дальнейшем сохранять индекс полюса в обозначении вектора угловой скорости, т.е.
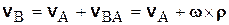 . (5.5)
. (5.5)
Так как 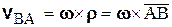 , то модуль скорости
, то модуль скорости
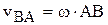 ,
,
ибо вектор 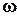 перпендикулярен плоскости чертежа. Отметим, что вектор
перпендикулярен плоскости чертежа. Отметим, что вектор 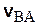 перпендикулярен также АВ. Направление вращения плоской фигуры вокруг полюса зависит только от знака проекции угловой скорости на ось
перпендикулярен также АВ. Направление вращения плоской фигуры вокруг полюса зависит только от знака проекции угловой скорости на ось
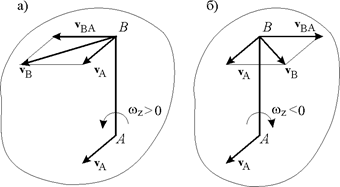 Рис. 5.4. Рис. 5.4. | Az 2. Так как 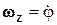 , то при , то при 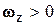 вращение происходит против хода часовой стрелки и при вращение происходит против хода часовой стрелки и при 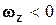 – по ходу часовой стрелки. На рис. 5.4 а и б показано, как, зная скорость – по ходу часовой стрелки. На рис. 5.4 а и б показано, как, зная скорость |
точки А, можно найти скорость точки В 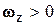 и
и 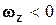 .
.
Из формулы (5.5) следует одна полезная теорема: При плоском движении проекции скоростей двух точек тела на ось, проходящую через эти точки, равны между собой.
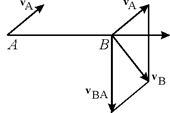 Рис. 5.5. Рис. 5.5. | Выберем положительное направление для оси АВ, как указано на рис. 5.5. Воспользуемся далее формулой (5.5) 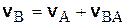 . . |
Проектируя это равенство на направление АВ, получим
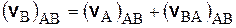 .
.
Последнее слагаемое в этом соотношении равно нулю, так как вектор 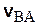 перпендикулярен АВ и, следовательно,
перпендикулярен АВ и, следовательно, 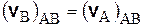 .
.
 2014-01-25
2014-01-25 1836
1836
