2014-01-25
744
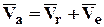
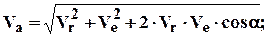
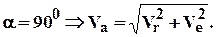
Абсолютное, относительное и переносное ускорения.
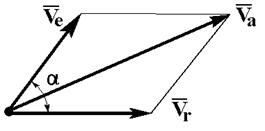
Ускорение движущейся точки по отношению к неподвижной системе отсчёта называется абсолютным - аа.
Ускорение движущейся точки по отношению к подвижной системе отсчёта называется относительным – аr.
Переносным ускорением точки называется ускорение такой точки, неизменно связанной с подвижной системой осей координат, с которой в данный момент совпала движущаяся точка – ае.
Теорема Кориолиса.
При переносном непоступательном движении абсолютное ускорение точки равно геометрической сумме её относительного, переносного и ускорения Кориолиса.
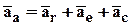
Ускорение Кориолиса
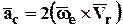
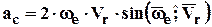
Направление вектора ас.
Вектор ас направлен по перпендикуляру, восстановленному из движущейся точки к плоскости векторов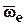 
и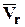 
(вектор 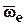необходимо параллельно самому себе перенести в движущуюся точку) в ту сторону, чтобы, глядя навстречу этому вектору видеть кратчайшее совмещение вектора 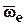с вектором 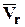происходящим против хода часовой стрелки.
Правило Жуковского. Чтобы показать вектор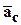 
необходимо вектор 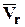спроецировать на плоскость вращения и полученную проекцию повернуть в сторону вращения на 900.
Пример:
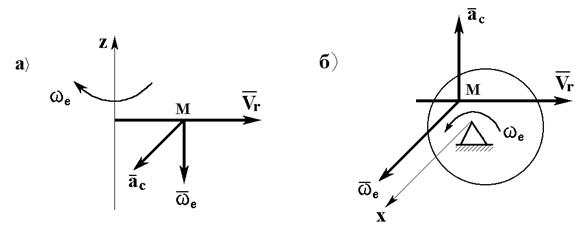
Ускорение Кориолиса равно 0, если:
1. 
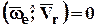или 1800;
2. wе = 0.
Следствие из теоремы Кориолиса:
при переносном поступательном движении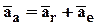 
;
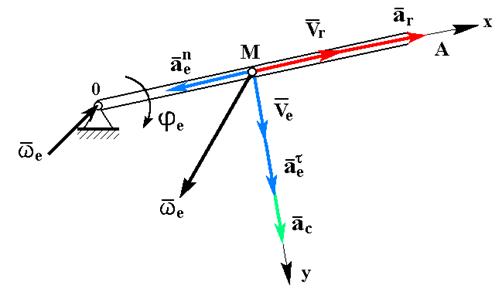
Задача № 1
ОМ = Sr = 2t2, м
jе = t3, рад
t = 1c
_______________
Va; aa -?
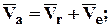
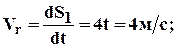
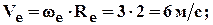
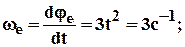
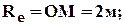
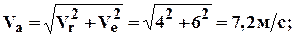
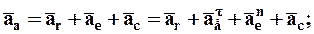
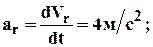
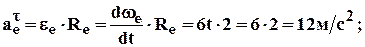
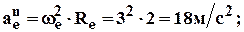
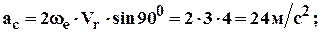
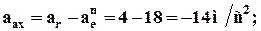
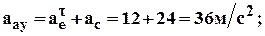
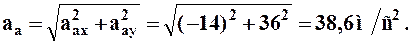
Задача № 2:
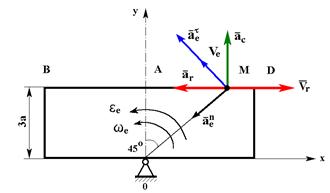
j = 4(t2 – t)
a = 0,12 м
t = 1 c
S = 0,5(3t – t2) – 0,64 _________________
a; V;
1. Определим положение точки М:
S = 0,5(3 – 1) – 0,64 = 1 – 0,64 = 0,36 м;
OA = 0,36 м; AМ = 0,36 м;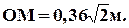 
2. Относительное движение:
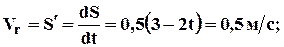
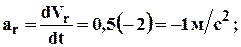
3. Переносное движение:
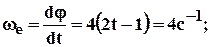
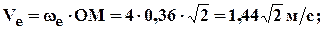
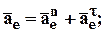
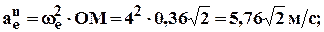
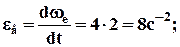
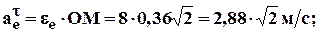
4. Ускорение Кориолиса:
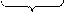
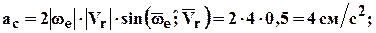
sin90о = 1
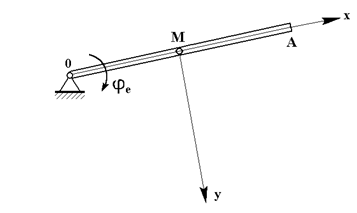
5. Абсолютная скорость и абсолютное ускорение:
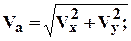
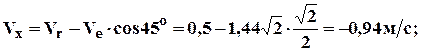
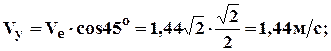
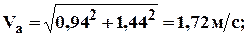
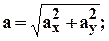
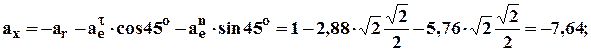
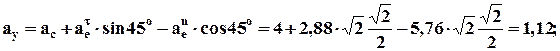
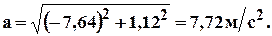
Плоскопараллельное движение твёрдого тела.
