2014-01-25
793
Рис. 2.12. Естественный трехгранник
Единичный вектор, направленный вдоль главной нормали внутрь траектории, обозначим буквой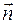 
. Единичный вектор 
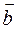, ортогональный соприкасающейся плоскости и направленный в ту сторону, откуда поворот от 
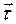‚ к 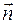виден происходящим против хода часовой стрелки, определяет направление бинормали 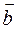. Плоскость, образуемая векторам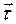и и 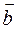, называется спрямляющей плоскостью.
Система координат, образуемая тремя взаимно ортогональными осями- касательной, нормалью и бинормалью, называется естественной системой координат. Трехгранник, образуемый соприкасающейся, нормальной и спрямляющей плоскостями называется естественным или подвижным трехгранником. Перемещаясь вместе с движущейся точкой М, оси этого подвижного трехгранника меняют свою ориентацию в пространстве, оставаясь взаимно ортогональными.
Пример. Движение точки М задано уравнениями
, 
,
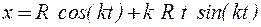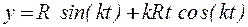где k - постоянная.
Определить модули скорости и ускорения как функции времени.
Решение: Дважды дифференцируя уравнения движения по времени, получаем
,
,
,
.
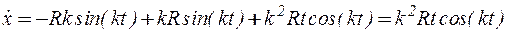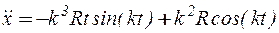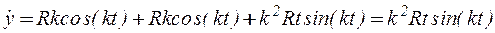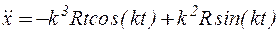Подставляя найденные значения производных в формулы (8) и (14), получаем:
, 
.
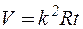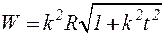Лекция 12
