Движение тела характеризуется скоростью и ускорением, которые могут изменяться во времени. Пусть материальная точка движется по плоской криволинейной траектории с переменной по величине и направлению скоростью (рис. 4). Для характеристики степени криволинейности вводится понятие радиуса кривизны в данной точке траектории.
Радиусом кривизны R траектории называют радиус окружности, которая сливается с криволинейной траекторией на бесконечно малом ее участке.
В данной точке траектории касательная всегда перпендикулярна радиусу кривизны.
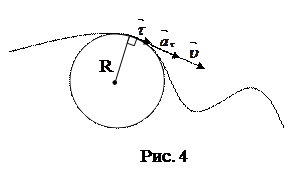
Пусть и скорость, и ускорение меняются по величине и направлению.
Мы знаем, что ускорение тела при движении есть 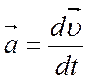 .
.
Вектор скорости 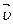 можно представить как произведение модуля скорости
можно представить как произведение модуля скорости 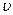 и некоторого единичного вектора
и некоторого единичного вектора 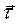 , сонаправленного с вектором линейной скорости
, сонаправленного с вектором линейной скорости 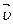 , направленного по касательной к траектории.
, направленного по касательной к траектории.
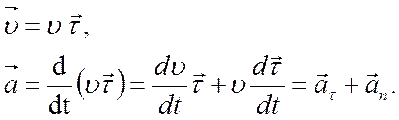
Таким образом, полное ускорение материальной точки при криволинейном движении можно представить в виде суммы двух слагаемых. Первое слагаемое 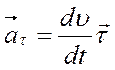 .
.
Вектор 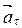 направлен по касательной к траектории и называется тангенциальным или касательным ускорением. Его модуль равен
направлен по касательной к траектории и называется тангенциальным или касательным ускорением. Его модуль равен 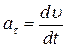 , поэтому
, поэтому 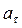 характеризует быстроту изменения скорости криволинейного движения только по величине, так как вектор
характеризует быстроту изменения скорости криволинейного движения только по величине, так как вектор 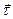 не изменяется.
не изменяется.
Следовательно, можно заключить, что 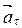 - тангенциальное ускорение, характеризует изменение скорости по величине и направлено по касательной к траектории.
- тангенциальное ускорение, характеризует изменение скорости по величине и направлено по касательной к траектории.
Второе слагаемое 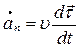 называется нормальным ускорением.
называется нормальным ускорением.
Так как вектор 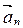 сонаправлен с вектором
сонаправлен с вектором 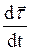 , который определяет изменение направления вектора линейной скорости, то он характеризует изменение скорости криволинейного движения по направлению.
, который определяет изменение направления вектора линейной скорости, то он характеризует изменение скорости криволинейного движения по направлению.
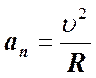 .
.
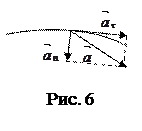
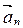 перпендикулярно скорости, направлено вдоль радиуса кривизны траектории к центру окружности.
перпендикулярно скорости, направлено вдоль радиуса кривизны траектории к центру окружности.
Полное ускорение материальной точки при криволинейном движении характеризует быстроту изменения скорости как по величине, так и по направлению (рис.6).
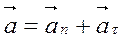 ,
, 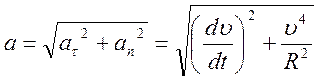 .
.
 2014-01-25
2014-01-25 3911
3911
