Определение скорости и ускорения точки

Скорость и ускорение при координатном способе задания движения

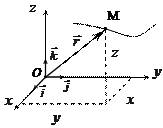Связь векторного способа задания движения и координатного дается соотношением .

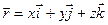Из определения скорости:

.

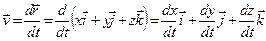Проекции скорости на оси координат равны производным соответствующих координат по времени , , .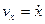

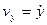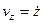Точкой сверху здесь и в дальнейшем обозначается дифференцирование по времени.

Модуль и направление скорости определяются выражениями:

, , , .

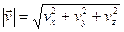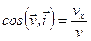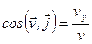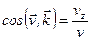Из определения ускорения:

.

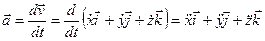Проекции ускорения на оси координат равны вторым производным соответствующих координат по времени ,, .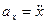

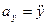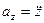Модуль и направление ускорения определяются выражениями:

,

, , .

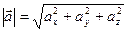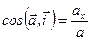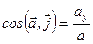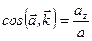Скорость и ускорение при естественном способе задания движения

Естественные оси (касательная, главная нормаль, бинормаль) – это оси подвижной прямоугольной системы координат с началом в движущейся точке. Их положение определяется траекторией движения.

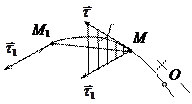Касательная (с единичным вектором 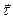) направлена по касательной в положительном направлении отсчета дуговой координаты и находится как предельное положение секущей, проходящей через данную точку.

Через касательную проходит соприкасающаяся плоскость, которая находится как предельное положение плоскости p при стремлении точки M₁ к точке M. Нормальная плоскость перпендикулярна касательной. Линия пересечения нормальной и соприкасающейся плоскостей – главная нормаль. Единичный вектор главной нормали 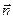направлен в сторону вогнутости траектории.

Бинормаль с единичным вектором 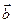направлена перпендикулярно касательной и главной нормали так, что ос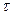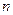и , и 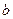образуют правую систему координат.

Координатные плоскости введенной подвижной системы координат (соприкасающаяся, нормальная и спрямляющая) образуют естественный трехгранник, который перемещается вместе с движущейся точкой, как твердое тело. Его движение в пространстве определяется траекторией и законом изменения дуговой координаты.

Определение скорости и ускорения точки при естественном способе задания движения

Из определения скорости точки

,

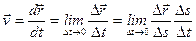где 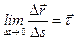, 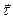– единичный вектор касательной.

Тогда:

, .

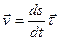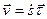Алгебраическая скорость 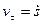– проекция вектора скорости на касательную, равная производной от дуговой координаты по времени. Если производная положительна, то точка движется в положительном направлении отсчета дуговой координаты.

Из определения ускорения

,

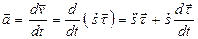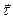– переменный по направлению вектор и .

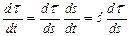Производная 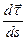определяется только свойствами траектории в окрестности данной точки,

при этом ,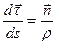

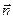– единичный вектор главной нормали,

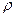– радиус кривизны траектории в данной точке.

Таким образом 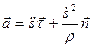, т.е. вектор ускорения раскладывается на две составляющие – касательное и нормальное ускорения.

, , ,

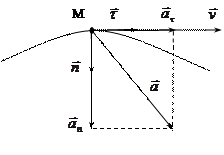
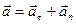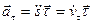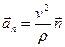где 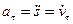– алгебраическое значение касательного ускорения (проекция вектора ускорения на касательную) характеризует изменение скорости по величине;

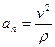– нормальное ускорение (проекция вектора ускорения на нормаль) характеризует изменение скорости по направлению.

Вектор ускорения всегда лежит в соприкасающейся плоскости и проекция ускорения на бинормаль равна нулю ().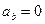

Движение точки ускоренное, если знаки проекций векторов скорости и ускорения на касательную совпадают.